Приклади обчислення ємності

(Калашников, Сивухин)

При всіх розрахунках ємності будемо користуватись означенням ємності 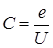і готовими виразами для потенціалів, які ми отримали раніше.

Ємність плаского конденсатора. Отримали його вище.

.

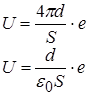
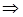
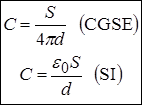Ємність ізольованої кулі. Потенціал кулі зовні співпадає із потенціалом точкового заряду.

.

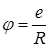
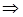
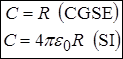Ємність сферичного конденсатора.

.

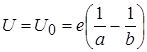
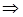
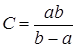Ємність циліндричного конденсатора (коаксиал).

.

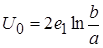
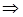
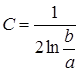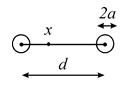
Ємність двопровідної лінії. Дві тонкі провідні лінії радіусом 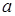розташовані на відстані 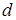. Лінії заряджені протилежними зарядами. Поля від кожної лінії додаються:

,

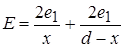де координата точки між лініями. Тоді потенціал у цій точці

.

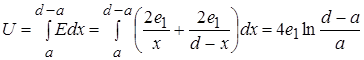Звідси ємність

,

оскільки 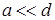(провідники тонкі і знаходяться на відносно великій відстані).

Енергія електричного поля, її локалізація в просторі

Давайте домовимось, що для системи заряджених тіл будемо розрізняти три типи потенціальної енергії: власна енергія кожного із тіл , взаємна енергія заряджених тіл 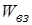і повна енергія .

Уявимо собі такий процес. Беремо систему незаряджених тіл, розносимо їх на велику відстань одне від одного, а потім заряджаємо кожне з них. При зарядженні ми виконуємо роботу 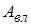, підносячи до зарядженого тіла все нові порції заряду і долаючи сили кулонівського відштовхування. Оскільки робота виконується над зарядом, 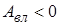, тому власна енергія зарядженого тіла дорівнює витраченій роботі із зворотним знаком і завжди додатня. Дійсно, згадайте перше начало термодинаміки

; ; .

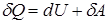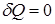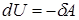Отже, із загальних міркувань, сумарна власна енергія 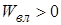незалежно від знаків зарядів тіл. Далі ми покажемо це строго, таку задачу розв’язує Річард Фейнман у своїх лекціях, т.5.

Тепер будемо зближувати заряджені тіла до тієї відстані, на якій вони знаходяться в конкретній задачі. Для цього також необхідно виконати роботу, однак її знак може бути як додатним, так і від’ємним. Дійсно, зближуючи два однаково заряджених тіла, ми виконуємо від’ємну роботу 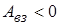проти сил відштовхування, а внесок у взаємну енергію буде додатним 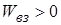. Якщо зближуються різнойменно заряджені тіла, то внесок в буде від’ємним 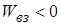. Далі ми доведемо, що повна енергія , власна енергія – 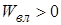додатна величина, а взаємна енергія 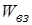може мати різний знак.

Спочатку будемо визначати взаємну енергію зарядів.

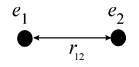1. Почнемо з розрахунку взаємної енергії двох точкових зарядів 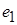і 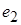, які знаходяться на відстані 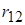один від одного. Для цього можна закріпити один із зарядів (наприклад, 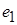), а другий (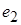) перенести із нескінченності в точку на відстані 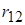від першого.

Заряд 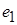створює у просторі електростатичне поле, потенціал якого на відстані 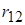дорівнює 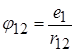. Що таке потенціал? За означенням: потенціал чисельно дорівнює роботі, що виконує поле при віддаленні одиничного позитивного заряду на нескінченність.

А якщо віддаляється не одиничний заряд? Робота становитиме 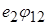. А якщо він не віддаляється, а наближається до околу заряду 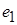? Тоді робота становитиме 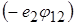. А енергія? Енергія дорівнюватиме роботі із протилежним знаком

.

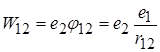Можна закріпити 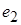і переміщати 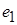, тоді

.

де 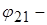потенціал, який створює заряд 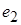в точці, де знаходиться 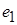.Очевидно, що

,

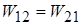тому

,

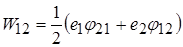або, позначивши 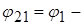як потенціал у точці знаходження першого заряду, як потенціал у точці знаходження другого заряду,

.

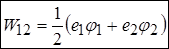Ми отримали вираз для взаємної енергії двох точкових зарядів. Зверніть увагу на двійку у знаменнику. З нею ви зустрінетесь і у системі багатьох зарядів. Кожен із доданків сам по собі вже є енергією взаємодії. Ми могли виразити її через будь-який з них. Але двійка потрібна для того, щоб кожну пару зарядів враховували лише раз, а не два рази. Це буде актуально у наступній задачі.

2. Перейдемо до системи багатьох точкових зарядів. Нехай маємо 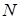точкових зарядів.

Для двох зарядів 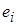і , які знаходяться на відстані , взаємна енергія

;

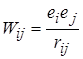енергія i –го заряду в полі інших

;

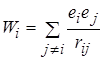взаємна енергія системи

.

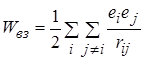Ось і виліз коефіцієнт 1/2, щоб запобігти подвійному підсумовуванню, оскільки

.

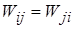Перепишемо енергію у вигляді

.

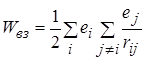Введемо позначення

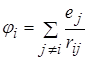
Це потенціал, який створюється усіма зарядами, крім 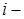го, в точці, де знаходиться 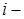заряд. В результаті маємо

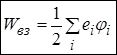
енергію системи точкових зарядів.

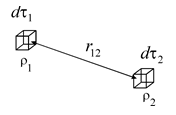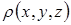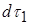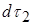3. Ще ускладнимо собі задачу. Нехай заряд неперервно розподілений у просторі з об’ємною густиною . Тоді в просторі, де знаходиться заряд, можна виділити два нескінченно малих елементи об’єму і на відстані 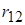один від одного. Оскільки елементарні заряди виділених об’ємів

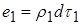та ,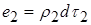

їх взаємна енергія

.

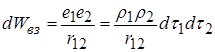Взаємна енергія всієї системи визначається інтегруванням по всьому об’єму, і тут так само треба унеможливити подвійне інтегрування множником :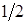

.

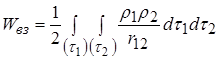По аналогії із тим, як ми вводили потенціал для системи точкових зарядів, введемо

.

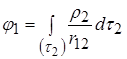Це потенціал, який створюється всім об’ємом в елементарному об’ємі 1. Тоді

,

або позбавившись індексів

. (*)

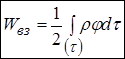Заряд може бути розподіленим на площині або вздовж лінії. Для них енергія виглядатиме, відповідно

; ,

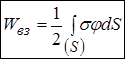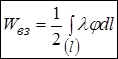де відповідно площинна (поверхнева) та лінійна густина заряду.

Ми отримали вирази для енергії для різних випадків. Що у них є спільного? Входить заряд (або його густина) та потенціал, створений у точці розташування заряду. Тепер ми однозначно можемо визначити знак взаємної енергії. Очевидно, що у випадку однойменних зарядів 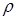і 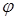матимуть однаковий знак, і 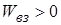. Відповідно, у випадку різнойменних зарядів 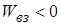. Тобто, отримали те, що і раніше із інших міркувань (через роботу).

Крім того, отриманий вираз (*) дозволяє зробити висновок про локалізацію енергії. Де знаходиться енергія? Формула свідчить – там, де є заряд.

Давайте підійдемо до проблеми знаходження енергії електростатичного поля з іншого боку.

Візьмемо поле плаского конденсатора. Задача добре знайома і зручна.

Площа пластин його 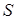, відстань між ними 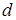набагато менша за лінійні розміри пластин. Це означає, що крайовими ефектами ми можемо знехтувати, і поле в конденсаторі є сталим і однорідним.

Пластини заряджені із поверхневою густиною заряду і 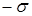. Різниця потенціалів між ними . Тоді за отриманою формулою для енергії

.

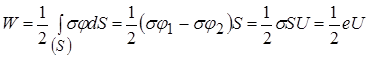Інтегрування було непотрібне, оскільки 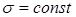. Ми отримали корисну формулу для енергії плаского конденсатора, яку можна записати у кількох виглядах

.

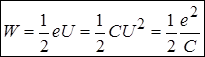З іншого боку, поле плаского конденсатора , , , , 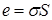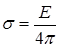тому

,

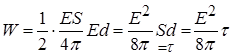де 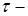об’єм проміжку між пластинами конденсатора. Величина

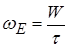
являє собою енергію, що припадає на одиницю об’єму конденсатора. Тобто ми можемо ввести поняття об’ємної густини енергії електростатичного поля

в системі CGSE,

тобто це енергія одиниці об’єму.

Провівши аналогічні обчислення в системі СІ, де

; ,

отримаємо

.

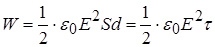Тоді об’ємна густина енергії

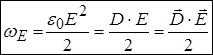в системі СІ.

Навіщо нам було розглядати цей частинний випадок? А він виявляється дуже для нас корисним у подальшому.

Тепер підемо від частинного до загального. Погодьтеся що ми завжди можемо зробити таку процедуру. При будь-якій конфігурації еквіпотенціальних поверхонь ми завжди можемо вибрати дві нескінченно близькі еквіпотенціальні поверхні. Між ними виберемо невеликий об’єм 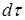таким чином, що еквіпотенціальні поверхні будуть паралельними. Вони утворять плаский конденсатор об’ємом 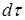із густиною об’ємної енергії 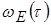. Енергія, що запасена у такому конденсаторі

.

Повна енергія системи є інтегралом по об’єму

. (**)

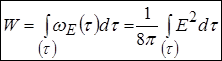Отже, отриманий зв’язок між густиною енергії і напруженістю електростатичного поля є універсальним, оскільки будь-яке поле можна уявити як систему пласких конденсаторів між еквіпотенціальними поверхнями, по яких треба інтегрувати. Тобто отриманий у частинному випадку для плаского конденсатора результат можна розповсюдити на довільне електростатичне поле.

Тепер зверніть увагу, ми тут не розділяємо, про яку енергію йде мова. У випадку конденсатора ми шукали повну енергію. Оскільки знакозмінною величиною тут є тільки напруженість електричного поля, а вона входить у формулу у квадраті, то повна енергія системи є додатньою величиною .

Зупинимось на фізичному змістові отриманого рівняння (**) для енергії. Вираз пов’язує енергію з вектором напруженості електричного поля. Енергія локалізована повсюди, де є електростатичне поле.

Отже, ми одержали два вирази для повної енергії електростатичного поля:

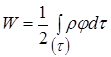і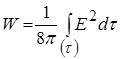

Ці вирази еквівалентні, тому що одержані одне з одного. Однак, фізичний зміст, закладений в них, різний.

Перший вираз зумовлює інтегрування по тій області простору, де присутній заряд 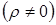. Його фізичний зміст у тому, що в електростатичному полі енергія локалізована там, де є заряд. Там же, де 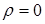, енергія відсутня.

Другий вираз пов’язує енергію з вектором напруженості електричного поля. Енергія знаходиться повсюди, де є поле. В електростатиці можна користуватися будь-яким з цих виразів.

Так, наприклад, сподіваюсь, на семінарах ви будете розв’язувати таку задачу. Є рівномірно заряджена з об’ємною густиною 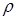куля з радіусом .

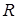За першим виразом енергія локалізована тільки всередині кулі і інтегрувати треба лише по об’єму кулі.

За другим виразом енергія знаходиться як всередині, так і зовні кулі, тому що поле є і при 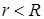, і при 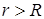. Обчислення дають однаковий результат

.

Оскільки питання про еквівалентність цих виразів є принциповим, покажемо це строго (Фейнмановские лекции по физике, т.5).

Візьмемо вираз для енергії у вигляді

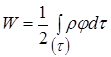
і скористуємось рівнянням Максвелла 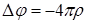. Тоді

.

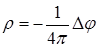Підставимо густину заряду у вираз для енергії

.

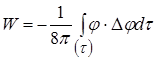Перетворимо окремо вираз

.

Скористаємось штучним прийомом (використовували і у молекулярній фізиці)

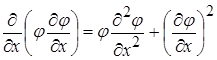, звідки .

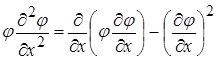Тоді для всіх трьох координат

.

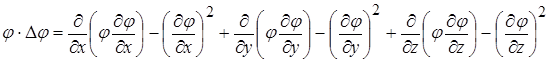Остаточно, згорнувши добре відомі вирази, маємо

.

Підставимо під знак інтегралу

.

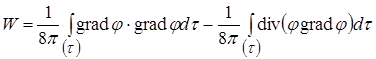Розглянемо спочатку другий доданок. Застосуємо до нього формулу Остроградського

.

Інтегрування повинно проводитись по всьому простору. Як залежать множники під інтегралом від відстані? При значних розмірах простору заряджене тіло можна розглядати як точкове:

; ; ; ; .

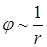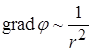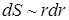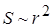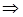
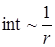Інтеграл буде обернено пропорційний відстані. При інтегруванні по всьому простору 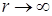, тому . Отже, другим доданком у виразі для енергії нехтуємо.

Скористаємось тим, що . Тоді

,

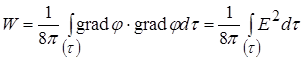що й треба було довести. Із одного з виразів для енергії ми отримали другий.

Отже, в електростатиці обидва вирази для енергії еквівалентні, ними обома можна користуватись. Однак, коли ми переходимо до змінних електричних полів, єдиним правильним виразом є вираз 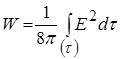. Підтвердженням цьому є те, що радіо та телепередачі можливі тому, що ми передаємо енергію через простір, де немає зарядів, але існує поле.

Тепер, користуючись отриманим рівнянням (**), ми можемо повернутись до енергії поля точкового заряду. Поле точкового заряду задля різноманітності візьмемо у системі СІ

.

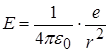Тоді об’ємна густина енергії становитиме

.

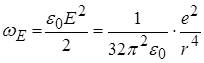Для інтегрування виберемо елементарний об’єм у вигляді сферичного шару

.

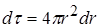Звідси маємо вираз для повної енергії поля точкового заряду

.

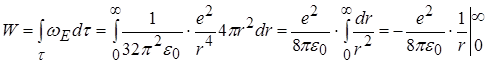А ось тут вже починаються фокуси. Підстановка верхньої межі не викликає складнощів, відповідний доданок буде дорівнювати нулю. Але оскільки заряд у нас точковий, тобто не має розміру, то інтегрувати треба від нуля. Виходить така нісенітниця, що енергія точкового заряду є нескінченною. До речі, цей же результат можна отримати, спрямувавши до нуля радіус рівномірно зарядженої кулі .

Ми змушені прийти до висновку, що уявлення про те, що енергія локалізована у місцях існування електростатичного поля не узгоджується з уявленнями про існування точкових зарядів. Один із шляхів подолання цієї проблеми – вважати елементарні заряди не точками, а невеликими зарядженими областями. Інший – вважати некоректною нашу теорію електрики на малих відстанях. Можна придумати ще варіанти. Але всі ці шляхи все одно приводять до певних утруднень, які досі ще подолати не вдалось.

Зв’язок енергії електростатичного поля з пондеромоторними силами

Давайте згадаємо, як ми вводили поняття напруженості електростатичного поля. Це було відношення сили, що діє на пробний заряд, до величини даного заряду 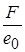. Отже, напруженість електростатичного поля – це сила, що діє з боку поля на одиничний позитивний заряд у вакуумі. Тобто на заряд діє сила. Ця сила відноситься до класу пондеромоторних (тобто механічних) сил, які діють на вагомі тіла (електрон же має масу?). Цей термін ввели, коли фізика ще визнавала наявність невагомих субстанцій, таких як теплород, ефір, електрична і магнітна рідина, тощо. Тепер він застарів, оскільки відсутність цих субстанцій доведена, але, як пише Сивухін, термін залишився за відсутності кращого.

Причиною виникнення пондеромоторних сил є електричні заряди, які надаються тілам. Але це надання заряду ускладнюється виникненням поляризаційних зарядів та пружних деформацій у провідниках і діелектриках. Розрахунок пондеромоторних сил з одночасним дослідженням механізму їх виникнення є достатньо складною задачею.

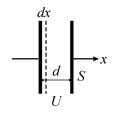Розглянемо виникнення пондеромоторних сил на простому прикладі плаского конденсатора.

Візьмемо плаский конденсатор з пластинами площею 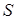, які знаходяться на відстані 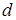. Між пластинами діє сила притягання 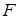. Припустимо, що внаслідок дії сили притягання одна з пластин відносно другої змістилась на відстань 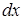. При цьому буде виконана робота

.

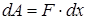З іншого боку, за першим началом термодинаміки (або законом збереження енергії) виконана робота дорівнює зміні енергії із протилежним знаком, тобто

.

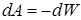При зміні відстані між пластинами при фіксованій напрузі на конденсаторі зміниться його ємність. Тоді виберемо вигляд для енергії плаского конденсатора у вигляді

.

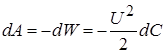Ємність плаского конденсатора 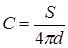. Оскільки змінною величиною є відстань між пластинами, то

.

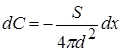Отже, вираз для роботи набуває вигляду

.

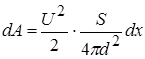Порівнявши вирази для роботи через силу та через енергію, маємо вираз для пондеромоторної сили (сили взаємодії пластин)

.

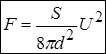Сила залежить від розмірів конденсатору (площа пластин, відстань між ними) і прямо пропорційна квадрату прикладеної до пластин напруги.

Давайте скористаємось тим, що для однорідного електростатичного поля в конденсаторі , і перейдемо до поля у виразі для сили:

.

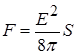А що таке 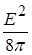? Це не що інше як об’ємна густина енергії 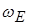, яку ми щойно отримали. Тоді силу можна виразити як

.

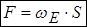Подивіться на останню формулу. Маємо, що сила прямо пропорційна площі. А що звичайно є коефіцієнтом пропорційності між силою і площею (згадайте молекулярну фізику)? Тиск. Тобто з одного боку 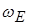є густиною енергії, а з іншої – тиском у електростатичному полі. У останньому випадку можемо позначити його 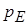. Тобто сила, яка діє на одиницю площі поверхні з боку електростатичного поля, дорівнює густині енергії цього поля.

Абсолютний вольтметр

Використовуючи отриману формулу зв’язку між силою і напругою, можна запропонувати конструкцію абсолютного вольтметра, тобто такого, який не потребує градуювання. (До речі, можна створити і абсолютний амперметр, що використовує протікання струму через електроліт.)

Абсолютний вольтметр являє собою важільні терези, на одну чашу яких можна покласти вантаж масою 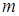, а друга чаша замінена пласким конденсатором. Конструкція такого вольтметру наведена на рисунку. Щоб крайові ефекти не впливали на виміри, одна з пластин складається з центральної частини з площею 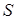і охоронного кільця, яке жорстко закріплене і має електричний зв’язок із центром. Такий пристрій забезпечує однорідне поле у центрі конденсатору.

Подавши на конденсатор вимірювану різницю потенціалів 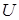і врівноваживши терези, маємо

,

звідки знаходимо напругу

.

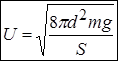Красива ідея? Чому ж ми її не використовуємо? Тому, що конструкція абсолютного вольтметру дозволяє проілюструвати ще одну особливість електростатичного поля. Легко переконатись, що рівновага, яку можна отримати в цьому вольтметрі, не є стійкою: достатньо пластинам конденсатору зблизитись за рахунок малих коливань або флуктуації , як внаслідок зменшення 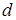сила притягання 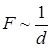зростає , і система стає неврівноваженою. Те ж саме відбувається і при зростанні 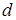: сила зменшується, і відстань продовжуватиме збільшуватись.

Як бачите, конструкція дуже проста, ідея красива, а використовувати – дзуськи. З технічної точки зору це утруднення можна усунути, якщо поставити два обмежувача та фіксувати вагу, яка переводить важіль терезів від одного обмежувача до другого. Момент відриву важеля від обмежувача можна вважати станом рівноваги. Але чомусь цим шляхом не йдуть, використовуючи зовсім неабсолютні вольтметри.

Date: 2015-09-24; view: 375; Нарушение авторских прав