Понятия о математических моделях и методах их решения

Одним из наиболее распространенных видов моделей в настоящее время является математическая модель. Математической моделью называется описание системы на каком-либо формальном языке, позволяющее выводить суждения о некоторых чертах ее поведения при помощи формальных процедур над ее описанием. При моделировании сложных систем обычно строятся их упрощенные математические модели, поскольку математическое описание не может быть всеобъемлющим и идеально точным.

Виды математических моделей весьма разнообразны — они могут представлять собой систему функциональных зависимостей между входными и выходными величинами системы; графики этих зависимостей; системы уравнений, описывающих движение систем; таблицы или графики переходов моделируемой системы из одного состояния в другое; алгоритмы и компьютерные программы, описывающие движение моделируемой системы.

Например, простейшая математическая модель перевозок, выполняемых грузовым автомобилем, может быть записана в виде:

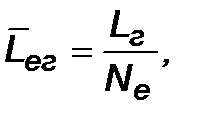(2.2)

где 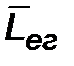— средняя длина ездки с грузом, км;

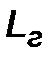— пробег с грузом, км;

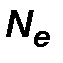— число ездок.

За время работы на линии автомобиль совершает определенное количество циклов транспортного процесса — ездок. Пробег за ездку состоит из пробега с грузом и пробега без груза.

Входными величинами такой модели являются значения пробега с грузом и число ездок, совершенных автомобилем, например, в течение смены. Среднее значение показателя пробега с грузом за ездку — выходная величина модели.

Изобразим эту же систему в форме графика переходов из одного состояния в другое (рис. 2.8).

В пунктах погрузки (точки 1) осуществляется проверка наличия груза, если груз отсутствует, то автомобиль переезжает под погрузку в другой пункт (точки 5 и 6). После разгрузки, если смена окончена, автомобиль возвращается в автотранспортное предприятие (точки 4).

Такую последовательность переходов состояния системы несложно реализовать в форме компьютерной программы — имитационной модели работы автомобиля — и проводить исследование показателей перевозок при различных (случайных) вариантах наличия или отсутствия грузов в пунктах погрузки. В реальных имитационных моделях исследуются показатели работы не отдельного автомобиля, а всего парка подвижного состава. При этом отдельные автомобили, функционирующие по схеме, представленной на рис. 2.8, совместно образуют сложную систему перевозок, состояния которой и переходы из одного состояния в другое уже сложно изобразить с такой же степенью детализации, как модель работы отдельного автомобиля. В системе перевозок появляются новые свойства, новые закономерности, которые не имеют смысла для отдельного автомобиля.

Рис. 2.8. Модель работы грузового автомобиля на линии

Date: 2015-09-24; view: 606; Нарушение авторских прав