Общая задача линейного программирования

Как построить линейную оптимизационную модель для решения реальной проблемы

Практика преподавания курса «Методы оптимизации транспортных процессов» показала, что наибольшие трудности у студентов вызывает не освоение и применение алгоритма симплексного метода, а формулирование оптимизационной модели по тексту задачи. Очевидно, что объективная сложность абстрагирования реальной (производственной) ситуации в виде целевой функции и системы ограничений является основной причиной недостаточно широкого использования методов линейной оптимизации на практике — в оперативной и проектной работе. Не в последнюю очередь это связано с тем, что в стандартных курсах «Линейное программирование» дается описание лишь общей планово-производственной задачи или задачи распределения ресурсов. Более сложные случаи, как правило, не рассматриваются. Поэтому сталкиваясь с необходимостью решить практическую оптимизационную задачу, инженер не в состоянии сформулировать для нее модель, обладая лишь умением строить модели для простейших случаев.

В этой главе дается общее описание методики построения линейных оптимизационных моделей, а также приводятся примеры построения модели для более сложных, чем задача распределения ресурсов, случаев.

Общая последовательность построения математической модели следующая:

1. Составление математической модели начинается с выбора переменных или неизвестных задачи, значения которых требуется определить для достижения минимума (затрат, расхода материалов, ресурсов и т.д.) или максимума (дохода или прибыли, объема производства или перевозок). При этом следует иметь ввиду, что иной раз от удачного выбора этих переменных зависит простота модели и, следовательно, удобство дальнейшего ее решения.

2. После выбора переменных необходимо составить по тексту задачи ограничения, которым эти переменные должны удовлетворять. При этом нужно следить, чтобы в модель были включены все ограничительные условия и в то же время не было ни одного лишнего.

3. На следующем этапе составляется целевая функция, которая является критерием выбора наилучшего значения переменных модели.

4. После составления математической модели необходимо ее упростить (по возможности) и выбрать подходящий вычислительный метод решения задачи. На данный момент рассмотрены три вычислительных метода: графический, общий симплексный и симплексный метод с искусственным базисом. Напомним, что графический метод применяется, если количество переменных не больше двух; общий симплексный — если неизвестных больше двух и система ограничений содержит только неравенства типа й; симплексный метод с искусственным базисом является наиболее универсальным и применяется, если система ограничений содержит уравнения или неравенства любого типа (2 и 5). причем в разных сочетаниях. В дальнейшем рассмотрим ряд методов, которые позволяют находить оптимальное решение специальных задач за меньшее число итераций. Специальные задачи — это частные случаи общей задачи линейного программирования, к которым относится, например, так называемая транспортная задача.

Начнем изучение методики создания линейных математических моделей с формулировки прямой и обратной общих задач линейного программирования. Порядок преобразования системы уравнений при переходе от прямой к обратной дескриптивной модели приводится во второй главе. Оптимизационная модель отличается от дескриптивной наличием критерия — целевой функции, следовательно, при переходе от прямой к обратной задаче линейного программирования преобразуется не только система ограничений, но и целевая функция.

Если прямая задача линейного программирования в общем виде записывается как

При условиях

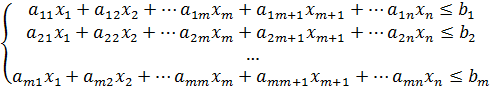
То обратная к ней задача запишется следующим образом:

При условиях

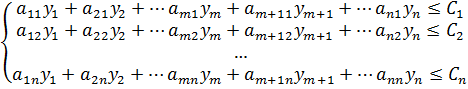
Прямая и обратная задачи могут быть интерпретированы следующим образом.

Прямая задача — сколько и какой продукции х необходимо произвести, чтобы при заданных стоимостях С единицы готовой продукции и размерах имеющихся ресурсов Ь, максимизировать доход от реализации продукции.

Двойственная задача — какова должна быть цена единицы каждого из ресурсов у, чтобы при заданных объемах ресурсов Ы и величинах стоимости единицы продукции С* общие затраты на производство были минимальными.

Если сформулирована математическая модель прямой задачи, то двойственную к ней задачу можно построить механически, используя следующие правила:

- в обратной задаче переменных у столько же, сколько уравнений в системе ограничений прямой задачи;

- матрица ограничений обратной задачи — это транспонированная матрица ограничений прямой задачи;

- в правой части уравнений системы ограничений обратной задачи стоят коэффициенты С, при неизвестных в целевой функции прямой задачи;

- коэффициентами при неизвестных в целевой функции обратной задачи являются правые части Ь, уравнений системы ограничений прямой задачи.

Date: 2015-09-24; view: 675; Нарушение авторских прав