Смысл волновой функции

Когда Шредингер впервые открыл свое уравнение, он открыл заодно, что закон сохранения есть следствие этого уравнения. Но он неправильно решил, что это плотность электрического заряда электрона, a 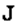– плотность электрического тока, т. е. он думал, что электроны взаимодействуют с электромагнитным полем через эти заряды и токи. Решая свои уравнения для атома водорода и вычисляя , он не вычислял никакой амплитуды (в то время еще не было амплитуд), а толковал это совершенно иначе. Атомное ядро было стационарно, вокруг же него текли токи; заряды и токи 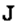генерировали электромагнитные поля, и все вместе это излучало свет. Но вскоре, решая задачу за задачей, он понял, что рассуждает не вполне правильно. И именно в этот момент Борн выдвинул весьма нетривиальную идею. Именно Борн правильно (насколько нам известно) отождествил в уравнении Шредингера с амплитудой вероятности, предположив, что квадрат амплитуды – это не плотность заряда, а всего лишь вероятность (на единицу объема) обнаружить там электрон и что если вы находите электрон в некотором месте, то там окажется и весь его заряд. Вся эта идея принадлежит Борну. Волновая функция электрона в атоме не описывает, стало быть, размазанного электрона с плавно меняющейся плотностью заряда. Электрон может быть либо здесь, либо там, либо где-то еще, но где бы он ни был, он всегда – точечный заряд. Но, с другой стороны, представим себе случай, когда огромное число частиц находится в одном и том же состоянии, очень большое их число с одной и той же волновой функцией. Что тогда? Одна из них будет здесь, другая – там, и вероятность обнаружить любую из них в данном месте пропорциональна 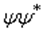. Но поскольку частиц так много, то, если я посмотрю в какой-нибудь объем , я, вообще говоря, обнаружу там примерно частиц. Итак, когда – волновая функция каждой из огромного количества частиц, поголовно пребывающих в одном и том же состоянии, то в этом случае 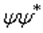можно отождествлять с плотностью частиц. Если в этих условиях все частицы несут одинаковые заряды 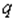, то мы можем пойти дальше и отождествить 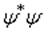с плотностью электричества. Обычно, если 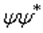имеет размерность плотности вероятности, то 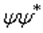надо умножить на 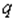, чтобы получить размерность плотности заряда. Для наших теперешних целей мы можем включить этот постоянный множитель в и принять за плотность электрического заряда само . Если помнить об этом, то 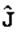(тот ток вероятности, который я вычислил) можно будет считать просто плотностью электрического тока. Итак, когда в одном и том же состоянии может находиться очень много частиц, возможно иное физическое толкование волновых функций. Плотность заряда и электрический ток могут быть вычислены прямо из волновых функций, и волновые функции приобретают физический смысл, который распространяется на классические, макроскопические ситуации. Нечто подобное может случиться и с нейтральными частицами. Если у нас имеется волновая функция отдельного фотона, то это – амплитуда того, что он будет обнаружен где-то. Хотя мы и не писали его, однако существует уравнение для фотонной волновой функции, аналогичное уравнению Шредингера для электрона. Фотонное уравнение попросту с овпадает с уравнениями Максвелла для электромагнитного поля, а волновая функция – с векторным потенциалом 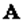. Волновая функция оказывается обычным векторным потенциалом. Физика квантов света совпадает с классической физикой, потому что фотоны суть невзаимодействующие бозе-частицы и многие из них могут пребывать в одинаковом состоянии; более того, как вы знаете, они любят бывать в одинаковом состоянии. В момент, когда мириады их окажутся в одном и том же состоянии (т. е. в одной и той же электромагнитной волне), вы сможете непосредственно измерить волновую функцию (т. е. векторный потенциал). Конечно, исторически все шло иным путем. Первые наблюдения были проведены при таких обстоятельствах, когда было много фотонов в одинаковом состоянии, и тем самым удалось открыть правильные уравнения для отдельного фотона, наблюдая непосредственно своими глазами природу волновой функции на макроскопическом уровне. Трудность с электроном состоит в том, что вы не можете поместить в одно и то же состояние больше одного электрона. Поэтому очень долго считалось, что волновая функция уравнения Шредингера никогда не будет иметь макроскопического представления, подобного макроскопическому представлению амплитуды для фотонов. Но теперь стало ясно, что явление сверхпроводимости представляет именно такой случай.

Вопрос

волна де бройля частицы, в каких случаях не стоит обсуждать волновые свойства частицы

Волны де Бройля
_{de Broglie waves}

Волны де Бройля – волны, связанные с любой движущейся материальной частицей. Любая движущаяся частица (например, электрон) ведёт себя не только как локализованный в пространстве перемещающийся объект - корпускула, но и как волна, причём длина этой волны даётся формулой λ = h/р, где h = 6.6·10^-34 Дж^.сек – постоянная Планка, а р – импульс частицы. Эта волна и получила название волны де Бройля (в честь французского физика-теоретика Луи де Бройля, впервые высказавшего гипотезу о таких волнах в 1923 г.). Если частица имеет массу m и скорость v << с (с – скорость света), то импульс частицы р = mv и дебройлевская длина волны связаны соотношением λ = h/mv.
Волновые свойства макроскопических объектов не проявляются из-за малых длин волн. Так для тела массой 200 г, движущегося со скоростью 3 м/сек, длина волны ≈10^-31 см, что лежит далеко за пределами наблюдательных возможностей. Однако для микрочастиц длины волн лежат в доступной наблюдению области. Например, для электрона, ускоренного разностью потенциалов 100 вольт, длина волны ≈10^-8 см, что соответствует размеру атома.
Для расчёта длины волны де Бройля частицы массы m, имеющей кинетическую энергию E, удобно использовать соотношение

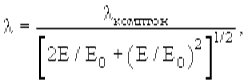
где E₀ = mc² − энергия покоя частицы массы m,
λ_{комптон} = h/mc − комптоновская длина волны частицы,
λ_{комптон} (электрон) = 2.4·10^-12 м = 0.024 Å,
λ_{комптон} (протон) = 1.32·10^-15 м = 1.32 фм.
Длина λ(фм) = h/p = hc/E = 2π·197 МэВ·фм /E(МэВ). волны де Бройля фотона с энергией Е определяется из соотношения

λ(фм) = h/p = hc/E = 2π·197 МэВ·фм /E(МэВ).

Существование волн де Бройля доказано многочисленными экспериментами, в которых частицы ведут себя как волны. Так при рассеянии пучка электронов с энергией 100 эВ на упорядоченной системе атомов кристалла, играющего роль дифракционной решётки, наблюдается отчётливая дифракционная картина. Существование волн де Бройля лежит в основе работы электронного микроскопа, разрешающая способность которого намного порядков выше, чем у любого оптического микроскопа, что позволяет наблюдать молекулы и атомы, а также в основе методов исследования таких сверхмалых объектов, как атомные ядра и элементарные частицы, бомбардировкой их частицами высоких энергий. Метод дифракции частиц в настоящее время широко используется при изучении строения и свойств вещества.

Вопрос

Принцип неопределенности Гейценберга

Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное соображение (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых, описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределённостей^{[* 1]} задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г., является одним из краеугольных камней физической квантовой механики.

Соотношения неопределённостей Гейзенберга являются теоретическим пределом точности одновременных измерений двух некоммутирующих наблюдаемых. Они справедливы как для идеальных измерений, иногда называемых измерениями фон Неймана, так и для неидеальных измерений.^{[* 2]}

Согласно принципу неопределённости у частицы не могут быть одновременно точно измерены положение и скорость (импульс)^{[* 3]}. Принцип неопределённости уже в виде, первоначально предложенном Гейзенбергом, применим и в случае, когда не реализуется ни одна из двух крайних ситуаций (полностью определенный импульс и полностью неопределенная пространственная координата — или полностью неопределенный импульс и полностью определенная координата).

Пример: частица с определённым значением энергии, находящаяся в коробке с идеально отражающими стенками; она не характеризуется ни определённым значением импульса (учитывая его направление!^{[* 4]}), ни каким-либо определённым «положением» или пространственной координатой (волновая функция частицы делокализована на всё пространство коробки, то есть её координаты не имеют определенного значения, локализация частицы осуществлена не точнее размеров коробки).

Соотношения неопределённостей не ограничивают точность однократного измерения любой величины (для многомерных величин тут подразумевается в общем случае только одна компонента). Если её оператор коммутирует сам с собой в разные моменты времени, то не ограничена точность и многократного (или непрерывного) измерения одной величины. Например, соотношение неопределённостей для свободной частицы не препятствует точному измерению её импульса, но не позволяет точно измерить её координату (это ограничение называется стандартный квантовый предел для координаты).

Соотношение неопределенностей в квантовой механике в математическом смысле есть прямое следствие некоего свойства преобразования Фурье^{[* 5]}.

Существует точная количественная аналогия между соотношениями неопределённости Гейзенберга и свойствами волн или сигналов. Рассмотрим переменный во времени сигнал, например звуковую волну. Бессмысленно говорить о частотном спектре сигнала в какой-либо момент времени. Для точного определения частоты необходимо наблюдать за сигналом в течение некоторого времени, таким образом теряя точность определения времени. Другими словами, звук не может одновременно иметь и точное значение времени его фиксации, как его имеет очень короткий импульс, и точного значения частоты, как это имеет место для непрерывного (и в принципе бесконечно длительного) чистого тона (чистой синусоиды). Временно́е положение и частота волны математически полностью аналогичны координате и (квантово-механическому) импульсу частицы. Что совсем не удивительно, если вспомнить, что , то есть импульс в квантовой механике — это и есть пространственная частота вдоль соответствующей координаты.

В повседневной жизни мы обычно не наблюдаем квантовую неопределённость потому, что значение чрезвычайно мало, и поэтому соотношения неопределенностей накладывают такие слабые ограничения на погрешности измерения, которые заведомо незаметны Определение

Если имеется несколько (много) идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения 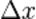координаты и среднеквадратического отклонения импульса, мы найдем что:

метны на фоне реальных практических погрешностей^{[* 6]} наших приборов или органов чувств.

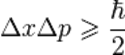
где ħ — приведённая постоянная Планка.

Отметим, что это неравенство даёт несколько возможностей — состояние может быть таким, что может быть измерен с высокой точностью, но тогда будет известен только приблизительно, или наоборот 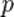может быть определён точно, в то время как — нет. Во всех же других состояниях и , и 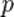могут быть измерены с «разумной» (но не произвольно высокой) точностью

Вопрос

Химическая связь, ковалентная и ионная связь, метод валентной связи для описания химической связи, гибридизация орбиталей

Химическая связь - это взаимодействие двух атомов, осуществляемое путем обмена электронами. При образовании химической связи атомы стремятся приобрести устойчивую восьмиэлектронную (или двухэлектронную) внешнюю оболочку, соответствующую строению атома ближайшего инертного газа. Различают следующие виды химической связи: ковалентная (полярная и неполярная; обменная и донорно-акцепторная), ионная, водородная и металлическая.

Ковалентная связь, атомная связь, гомеополярная связь (от лат. co — «совместно» и vales — «имеющий силу») — химическая связь, образованная перекрытием (обобществлением) пары валентных электронных облаков. Обеспечивающие связь электронные облака (электроны) называются общей электронной парой.

Термин ковалентная связь был впервые введён лауреатом Нобелевской премии Ирвингом Ленгмюром в 1919 году^[1][2]. Этот термин относился к химической связи, обусловленной совместным обладанием электронами, в отличие от металлической связи, в которой электроны были свободными, или от ионной связи, в которой один из атомов отдавал электрон и становился катионом, а другой атом принимал электрон и становился анионом.

Позднее (1927 год) Ф.Лондон и В.Гайтлер на примере молекулы водорода дали первое описание ковалентной связи с точки зрения квантовой механики.

С учётом статистической интерпретации волновой функции М.Борна плотность вероятности нахождения связывающих электронов концентрируется в пространстве между ядрами молекулы (рис.1). В теории отталкивания электронных пар рассматриваются геометрические размеры этих пар. Так, для элементов каждого периода существует некоторый средний радиус электронной пары (Å):

0,6 для элементов вплоть до неона; 0,75 для элементов вплоть до аргона; 0,75 для элементов вплоть до криптона и 0,8 для элементов вплоть до ксенона.^[3]

Характерные свойства ковалентной связи — направленность, насыщаемость, полярность, поляризуемость — определяют химические и физические свойства соединений.

Направленность связи обусловлена молекулярным строением вещества и геометрической формы их молекулы. Углы между двумя связями называют валентными.

Насыщаемость — способность атомов образовывать ограниченное число ковалентных связей. Количество связей, образуемых атомом, ограничено числом его внешних атомных орбиталей.

Полярность связи обусловлена неравномерным распределением электронной плотности вследствие различий в электроотрицательностях атомов. По этому признаку ковалентные связи подразделяются на неполярные и полярные (неполярные — двухатомная молекула состоит из одинаковых атомов (H₂, Cl₂, N₂) и электронные облака каждого атома распределяются симметрично относительно этих атомов; полярные — двухатомная молекула состоит из атомов разных химических элементов, и общее электронное облако смещается в сторону одного из атомов, образуя тем самым асимметрию распределения электрического заряда в молекуле, порождая дипольный момент молекулы).

Поляризуемость связи выражается в смещении электронов связи под влиянием внешнего электрического поля, в том числе и другой реагирующей частицы. Поляризуемость определяется подвижностью электронов. Полярность и поляризуемость ковалентных связей определяет реакционную способность молекул по отношению к полярным реагентам.

Электроны тем подвижнее, чем дальше они находятся от ядер.

Однако, дважды лауреат Нобелевской премии Л. Полинг указывал, что «в некоторых молекулах имеются ковалентные связи, обусловленные одним или тремя электронами вместо общей пары»^[2]. Одноэлектронная химическая связь реализуется в молекулярном ионе водорода H₂⁺.

Молекулярный ион водорода H₂⁺ содержит два протона и один электрон. Единственный электрон молекулярной системы компенсирует электростатическое отталкивание двух протонов и удерживает их на расстоянии 1,06 Å (длина химической связи H₂⁺). Центр электронной плотности электронного облака молекулярной системы равноудалён от обоих протонов на боровский Ковалентная связь образуется парой электронов, поделённой между двумя атомами, причём эти электроны должны занимать две устойчивые орбитали, по одной от каждого атома. ^[4]

A· + ·В → А: В

В результате обобществления электроны образуют заполненный энергетический уровень. Связь образуется, если их суммарная энергия на этом уровне будет меньше, чем в первоначальном состоянии (а разница в энергии будет ни чем иным, как энергией связи).

Заполнение электронами атомных (по краям) и молекулярных (в центре) орбиталей в молекуле H₂. Вертикальная ось соответствует энергетическому уровню, электроны обозначены стрелками, отражающими их спины.

Согласно теории молекулярных орбиталей, перекрывание двух атомных орбиталей приводит в простейшем случае к образованию двух молекулярных орбиталей (МО): связывающей МО и антисвязывающей (разрыхляющей) МО. Обобществленные электроны располагаются на более низкой по энергии связывающей МО.

радиус α₀=0,53 А и является центром симметрии молекулярного иона водорода H₂⁺.

Ионная связь — очень прочная химическая связь, образующаяся между атомами с большой разностью (>1,5 по шкале Полинга) электроотрицательностей, при которой общая электронная пара переходит преимущественно к атому с большей электроотрицательностью. Это притяжение ионов как разноимённо заряженных тел. Примером может служить соединение CsF, в котором «степень ионности» составляет 97 %. Рассмотрим способ образования на примере хлорида натрия NaCl. Электронную конфигурацию атомов натрия и хлора можно представить: 11 Na 1s2 2s2 2p 6 3s1; 17 Cl 1s2 2s2 2p6 Зs2 3р5 Это атомы с незавершенными энергетическими уровнями. Очевидно, для их завершения атому натрия легче отдать один электрон, чем присоединить семь, а атому хлора легче присоединить один электрон, чем отдать семь. При химическом взаимодействии атом натрия полностью отдает один электрон, а атом хлора принимает его. Схематично это можно записать так: Na — е —> Na⁺ ион натрия, устойчивая восьмиэлектронная 1s2 2s2 2p6 оболочка за счет второго энергетического уровня. Cl + е —> Cl^— — ион хлора, устойчивая восьмиэлектронная оболочка. Между ионами Na⁺ и Cl^— возникают силы электростатического притяжения, в результате чего образуется соединение. Ионная связь — крайний случай поляризации ковалентной полярной связи. Образуется между типичными металлом и неметаллом. При этом электроны у металла полностью переходят к неметаллу, образуются ионы.

Если химическая связь образуется между атомами, которые имеют очень большую разность электроотрицательностей (ЭО > 1,7 по Полингу), то общая электронная пара полностью переходит к атому с большей ЭО. Результатом этого является образование соединения противоположно заряженных ионов:

Между образовавшимися ионами возникает электростатическое притяжение, которое называется ионной связью. Вернее, такой взгляд удобен. На деле ионная связь между атомами в чистом виде не реализуется нигде или почти нигде, обычно на деле связь носит частично ионный, а частично ковалентный характер. В то же время связь сложных молекулярных ионов часто может считаться чисто ионной. Важнейшие отличия ионной связи от других типов химической связи заключаются в ненаправленности и ненасыщаемости. Именно поэтому кристаллы, образованные за счёт ионной связи, тяготеют к различным плотнейшим упаковкам соответствующих ионов.

Характеристикой подобных соединений служит хорошая растворимость в полярных растворителях (вода, кислоты и т. д.). Это происходит из-за заряженности частей молекулы. При этом диполи растворителя притягиваются к заряженным концам молекулы, и, в результате Броуновского движения, «растаскивают» молекулу вещества на части и окружают их, не давая соединиться вновь. В итоге получаются ионы, окружённые диполями растворителя.

При растворении подобных соединений, как правило, выделяется энергия, так как суммарная энергия образованных связей растворитель-ион больше энергии связи анион-катион. Исключения составляют многие соли азотной кислоты (нитраты), которые при растворении поглощают тепло (растворы охлаждаются). Последний факт объясняется на основе законов, которые рассматриваются в физической хим

Теория валентных связей (метод валентных связей, метод валентных схем, метод локализованных электронных пар) — приближённый квантовохимический расчётный метод, основанный на представлении о том, что каждая пара атомов в молекуле удерживается вместе при помощи одной или нескольких общих электронных пар.

Теория валентных связей заложена в 1927 году В.Гайтлером и Ф.Лондоном на примере квантовохимического расчёта молекулы водорода. В основе теории валентных связей лежит гипотеза о том, что при образовании молекулы из атомов, последние в значительной мере сохраняют свою электронную конфигурацию, а связывание атомов достигается в результате обмена электронов между ними и спаривания спинов двух электронов, находящихся на атомных орбиталях исходных атомов. Расчёт Гайтлера — Лондона оказался весьма значительным по своим результатам в развитии квантовой химии. В подтверждение электронной октетной теории (правило октета) Г.Льюиса было показано, что химическая связь в молекуле водорода действительно осуществляется парой электронов.

Электронная пара оказывается размазанной по всему пространству молекулы с различной плотностью, причём на линии связи между ядрами имеется сгущение электронной плотности по сравнению с другими областями пространства. Это сгущение электронной плотности на линии, связывающей ядра атомов, вызывает стягивающее действие на ядра и, соответственно, приводит к образованию химической связи (рис.1). Энергия связи определяется в основном обменным интегралом, величина которого существенно зависит от степени перекрывания атомных орбиталей атомов.

Date: 2015-09-22; view: 541; Нарушение авторских прав