Уравнение Дирака

Если уравнение Клейна –Гордона записать в виде (см (2.21))

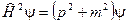, (2.23)

то уравнение Дирака, это ковариантное линейное уравнение вида

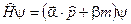(2.24)

или с учетом операторов и

(2.25)

Умножая это уравнение слева на 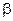получаем

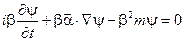(2.26)

полагая , и окончательно получаем ковариантную форму уравнения Дирака

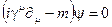(2.27)

где 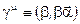- гамма-матрицы Дирака, .

, , ,

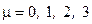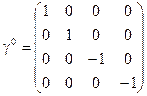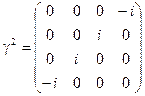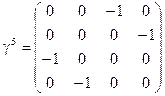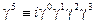
, используют также , (2.28)

Шпур (сумма диагональных элементов матрицы) нечетного числа 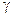–матриц равен нулю.

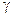–матрицы антикоммутативны: , .

Покажите: , , . , , , .

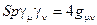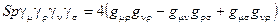Формально из уравнения Клейна-Гордона можно получить уравнение Дирака:

²ψ 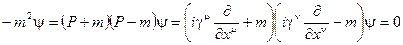(2.29)

Уравнение называется ковариантным, если оно имеет ту же форму после преобразований координат и функций. Уравнение Клейна-Гордона является ковариантным относительно преобразования Лоренца, и описывает частицы с целым спином (0,1). Уравнение Дирака является ковариантным, и описывает заряженные частицы со спином ½ (электроны и позитроны). Оба уравнения являются принципиально различными.

Уравнение Дирака –релятивистки инвариантное волновое уравнение описывающее частицы со спином ½ (электроны, мюоны и нейтрино). Предложено Дираком в 1928 г. В действительности уравнение Дирака представляет собой систему из четырех однородных линейных дифференциальных уравнений первого порядка для четырех волновых функций 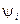(i=1,2,3,4) в совокупности описывающих состояние частицы. Например, нерелятивисткое уравнение Шредингера является уравнением для одной волновой функции .

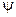Функция 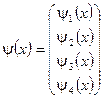называется спинорной волновой функцией дирковской частицы.

с помощью матриц Дирака система уравнений для свободной частицы записывается в матричном виде

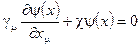(2.30)

где , . По дважды повторяющемуся индексу ведется суммирование: 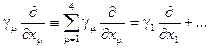, 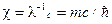- обратная комптоновская длина волны частицы с массой .

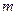Для матричных элементов волновой функции получаем четыре уравнения:

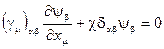, (2.31)

Используя представление Паули для гамма матриц получаем систему уравнений Дирака:

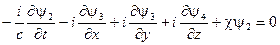
(2.32)

Используя оператор 4-импульса 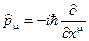, который является генератором трансляций уравнение Дирака можно переписать в виде

(2.33)

или

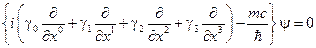(2.34)

Уравнение для определения собственных функций и собственных значений оператора следующее

(2.35)

где собственные значения операторов .

Волновая функция свободной частицы с импульсом 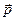и энергией Е описывается плоской волной де Бройля:

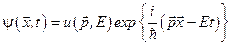(2.36)

С учетом (2.35) и (2.36) уравнение (2.34) может быть переписано в форме

(2.37)

где , .

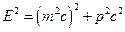При заданном значении импульса 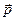существуют решения, соответствующие двум знакам энергии

(2.38)

Физический смысл существования решений отвечающих отрицательной энергии, разъясняется существованием частиц и античастиц. Все уровни с <0 и образуют «море Дирака», возмущение приводит к покиданию частицы (электрона) уровня с отрицательной энергией и образованию незанятого уровня- «дырки», соответствующей античастице (позитрону).

Тензор момента количества движения является генератором вращений.

Date: 2015-09-05; view: 559; Нарушение авторских прав