Уравнения Лагранжа

Уравнение Лагранжа для частиц, как известно, имеет вид:

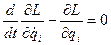, где 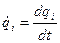(2.39)

здесь функция Лагранжа 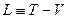, Функция Гамильтона .

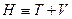где Т - кинетическая энергия системы, 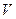-потенциальная энергия.

Для полей = 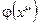(систем с непрерывно меняющими координатами)

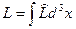, (2.40)

плотность оператора Лагранжа (Лагранжиан):

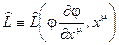(2.41)

Уравнения Эйлера- Лагранжа для полей следующие

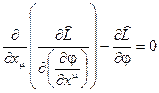(2.42)

Пример1. Лагранжиан 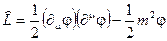при подстановке в уравнение (2.42) дает уравнение Клейна-Гордона

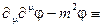(²- m ²)φ = 0

Пример2. Лагранжиан 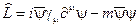приводит к уравнению Дирака при подстановке в (2.42). Каждая из четырех компонент волновых функци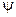й и 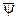рассматривается как независимая переменная.

Пример3. При подстановке лагранжиана 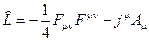в уравнение Эйлера- Лагранжа (2.42) получаются уравнения Максвелла:

,

где 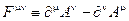, электронный ток .

Пример 4. В случае неабелевых (некоммутативных) калибровочных групп роль электромагнитного поля играют многокомпонентные поля 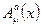, называемые полями Янга-Миллса. Уравнения Эйлера-Лагранжа для полей Янга-Миллса имеют вид

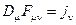, (2.43)

где ковариантная производная

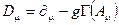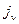, -ток полей материи,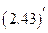

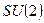
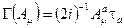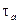для группы , где -матрицы Паули.(),

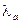для группы SU (3) , где -матрицы Гелл-Мана (),

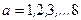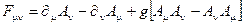- тензор напряженности поля Янга- Миллса, (2.44)

где 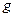-константа взамодействия. Физический смысл -тензор кривизны внутреннего пространства. Само поле Янга-Миллса описывает параллельный перенос в пространстве внутренней симметрии.

Действительное векторное поле описывает нейтральные частицы, комплексное векторное поле – заряженные частицы.

Лагранжиан квантовой электродинамики (КЭД)

При описании свойств и взаимодействий элементарных частиц вводится понятие физического поля, которое ставится в соответствие каждой частице. Физические поля состоят из отдельных порций –квантов. Математический ааапарат квантовой теории поля позволяет описать рождение и уничтожение частицы в каждой пространственно-временой точке. Для описания процессов происходящих с элементарными частицами в квантовой теории поля используется формализм Лагранжа. В Лагранжиане построенном из полей, участвующих во взаимодействии частиц, заключены все сведения о свойствах частиц и динамике их поведения. Лагранжиан состоит из лагранжиана описывающего поведение свободных полей и лагранжиана взаимодействия различных полей друг с другом.

В квантовой теории поля волновые функции частиц и полей становятся операторами. Теория квантовой электродинамики содержит одну заряженную частицу электрон со спином ½, являющийся фермионом и одну частицу поля со спином 1 - безмассовый векторный фотон, являющийся бозоном.

Лагранжиан (КЭД) представляет собой сумму кинетической энергии частиц электронного поля -первое слагаемое, кинетической энергии фотонного поля- третье слагаемое, и энергии взаимодействия электронного и фотонного полей -второе слагаемое:

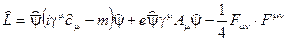(2.45)

здесь 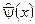-сопряженный оператор, уничтожает позитрон или рождает электрон в пространственно- временной точке х.

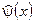- оператор, уничтожает электрон или рождает позитрон

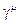-четыре матрицы Дирака , , , .

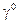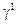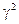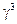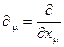-частная производная по 4-координате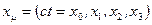

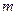-масса частицы(электрона), е - электрический заряд частицы.

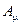- 4-потенциал фотонного поля

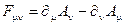-калибровочно- инвариантный тензор напряженности поля фотонов.

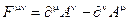-антисимметричный тензор электромагнитного поля

Слагаемое 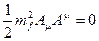в лагранжиане отсутствует, поэтому частица электромагнитного поля фотон безмассовая().

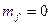Лагранжиан КЭД инвариантен относительно локального (в точке х) калибровочного преобразования электронного поля

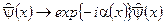, (2.46)

и фотонного поля

, (2.47)

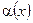-произвольная функция пространственных координат и времени.

Семейство фазовых преобразований 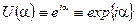образует унитарную абелеву группу, обозначаемую символом 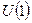. Абелевость выражается в том, что закон умножения рассматриваемой группы коммутативен

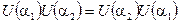. (2.48)

Date: 2015-09-05; view: 806; Нарушение авторских прав