Инерциальные системы отсчета

На рисунке представлен фрагмент игры в хоккей. В случае малого трения, обеспечиваемого гладкой поверхностью льда, брошенная шайба движется равномерно прямолинейно в течение достаточно длительного промежутка времени.

Первый закон Ньютона формулируется следующим образом: тело, неподверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называется свободным, а его движение – свободным движением или движением по инерции. Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии воздействия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции. Свободных тел, строго говоря, не существует. Однако естественно предположить, что чем дальше частица находится от других материальных объектов, тем меньшее воздействие они на нее оказывают. Представив себе, что эти воздействия уменьшаются, мы и приходим в пределе к представлению о свободном теле и свободном движении.

Экспериментально проверить предположение о характере движения свободной частицы невозможно, поскольку нельзя абсолютно достоверно установить факт отсутствия взаимодействия. Можно лишь с определенной степенью точности смоделировать данную ситуацию, используя экспериментальный факт уменьшения взаимодействия между удаленными телами. Обобщение ряда экспериментальных фактов, а также совпадение вытекающих из закона следствий с опытными данными доказывают его справедливость. При движении тело тем дольше сохраняет свою скорость, чем слабее на него действуют другие тела; например, скользящий по поверхности камень тем дольше движется, чем ровнее эта поверхность, то есть чем меньше воздействие на него этой поверхности.

Механическое движение относительно, и его характер зависит от системы отсчета. В кинематике выбор системы отсчета не был существенным. Не так обстоит дело в динамике. Если в какой-либо системе отсчета тело движется прямолинейно и равномерно, то в системе отсчета, движущейся относительно первой ускоренно, этого уже не будет. Отсюда следует, что закон инерции не может быть справедливым во всех системах отсчета. Классическая механика постулирует, что существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Такая система отсчета называется инерциальной системой отсчета (ИСО). Содержание закона инерции, в сущности, сводится к утверждению, что существуют такие системы отсчета, в которых тело, не подвергнутое внешним воздействиям, движется равномерно и прямолинейно или покоится.

Установить, какие системы отсчета являются инерциальными, а какие – неинерциальными, можно только опытным путем. Допустим, например, что речь идет о движении звезд и других астрономических объектов в доступной нашему наблюдению части Вселенной. Выберем систему отсчета, в которой Земля считается неподвижной (такую систему мы будем называть земной). Будет ли она инерциальной?

В качестве свободного тела можно выбрать звезду. Действительно, каждая звезда, ввиду ее громадной удаленности от других небесных тел, является практически свободным телом. Однако в земной системе отсчета звезды совершают суточные вращения на небесном своде, а следовательно, движутся с ускорением, направленным к центру Земли. Таким образом, движение свободного тела (звезды) в земной системе отсчета совершается по окружности, а не по прямой линии. Оно не подчиняется закону инерции, поэтому земная система отсчета не будет инерциальной.

Следовательно, для решения поставленной задачи надо проверить на инерциальность другие системы отсчета. Выберем в качестве тела отсчета Солнце. Такая система отсчета называется гелиоцентрической системой отсчета, или системой Коперника. Координатными осями связанной с ней системы координат являются прямые, направленные на три удаленные звезды, не лежащие в одной плоскости (рис. 2.1).

Таким образом, при изучении движений, происходящих в масштабе нашей планетной системы, а также всякой другой системы, размеры которой малы по сравнению с расстоянием до тех трех звезд, которые в системе Коперника выбраны в качестве опорных, система Коперника практически является инерциальной системой отсчета.

Пример

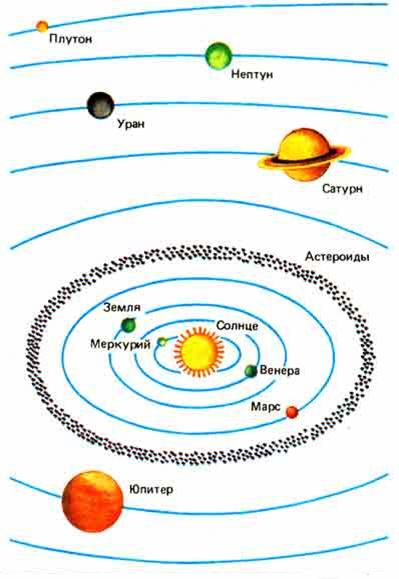
Траектории движения астрономических объектов Солнечной системы в гелиоцентрической системе отсчета

Неинерциальность земной системы отсчета объясняется тем, что Земля вращается вокруг собственной оси и вокруг Солнца, то есть движется ускоренно относительно системы Коперника. Так как оба эти вращения происходят медленно, то по отношению к громадному кругу явлений земная система ведет себя практически как инерциальная система. Вот почему установление основных законов динамики можно начать с изучения движения тел относительно Земли, отвлекаясь от ее вращения, то есть принять Землю за приблизительно ИСО.

Date: 2015-09-17; view: 716; Нарушение авторских прав