
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вещественные и мнимые корни знаменателя (метод Фостера)
|
|
Пусть в уравнении (6.2) F (p) представляет входное операторное сопротивление двухполюсника, 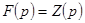 . Далее предположим, что все коэффициенты в (6.2) вещественны и положительны. Рассмотрим, как могут быть реализованы отдельные члены (6.2).
. Далее предположим, что все коэффициенты в (6.2) вещественны и положительны. Рассмотрим, как могут быть реализованы отдельные члены (6.2).
Слагаемое 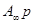 реализуется с помощью катушки с индуктивностью
реализуется с помощью катушки с индуктивностью 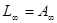 , т.к. операторное сопротивление для нее равно
, т.к. операторное сопротивление для нее равно 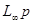 .
.
 Слагаемое
Слагаемое 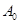 реализуется резистором с активным сопротивлением
реализуется резистором с активным сопротивлением 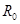
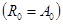 . Слагаемое
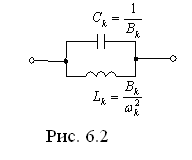
. Слагаемое 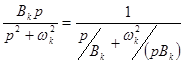 реализуется с помощью участка цепи, показанного на рис. 6.2.
реализуется с помощью участка цепи, показанного на рис. 6.2.
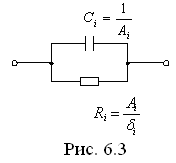
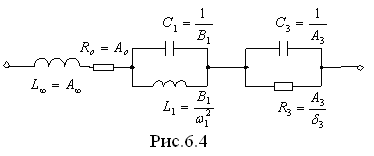
Слагаемое 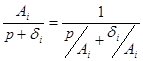 реализуется участком цепи, приведенном на рис. 6.3.
реализуется участком цепи, приведенном на рис. 6.3.
 Таким образом, для конкретного случая можно записать
Таким образом, для конкретного случая можно записать 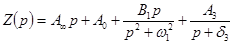 . Данное выражение соответствует цепи, показанной на рис. 6.4.
. Данное выражение соответствует цепи, показанной на рис. 6.4.
Пусть в соотношении (6.2) F (p) выражает входную операторную проводимость, 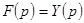 . Тогда слагаемое
. Тогда слагаемое 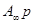 реализуется с помощью конденсатора
реализуется с помощью конденсатора 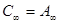 , т.к. операторная проводимость для него
, т.к. операторная проводимость для него 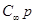 .
.
Слагаемое 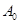 реализуется участком цепи с активной проводимостью
реализуется участком цепи с активной проводимостью 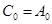 .
.
 Слагаемое
Слагаемое 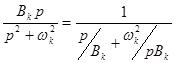 реализуется участком цепи, который показан на рис. 6.5,
реализуется участком цепи, который показан на рис. 6.5,
 т.к. операторная проводимость для него равна
т.к. операторная проводимость для него равна
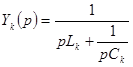 .
.
Слагаемое 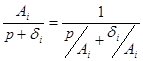 реализуется участком цепи (рис. 6.6),
реализуется участком цепи (рис. 6.6),
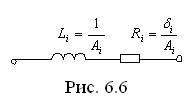 т.к. его операторная проводимость определяется следующим выражением
т.к. его операторная проводимость определяется следующим выражением 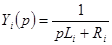 .
.
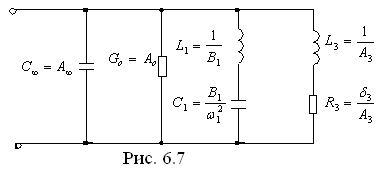 Таким образом, для конкретного случая можно записать
Таким образом, для конкретного случая можно записать 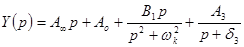
и в соответствии с этим выражением имеем следующую цепь (рис. 6.7).
В некоторых частных случаях при отрицательном значении 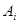 возможна реализация с помощью выражения (6.2), если
возможна реализация с помощью выражения (6.2), если 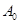 - достаточно большая величина
- достаточно большая величина
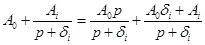 .
.
Если 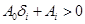 , то слагаемое
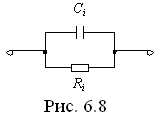
, то слагаемое 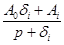 реализуется в виде схемы (рис. 6.8)
реализуется в виде схемы (рис. 6.8)
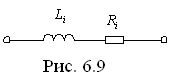
либо в виде схемы, показанной на рис. 6.9.
 Дробь
Дробь 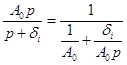 в случае
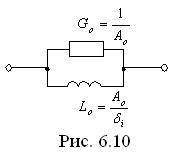
в случае 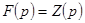 реализуется участком цепи (рис. 6.10), т.к. для него
реализуется участком цепи (рис. 6.10), т.к. для него
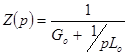 .
.
 В случае
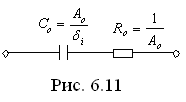
В случае 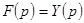 эта дробь реализуется следующей цепью (рис. 6.11).
эта дробь реализуется следующей цепью (рис. 6.11).
Рассмотрим пример реализации 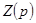 . Принято сопротивление R,
. Принято сопротивление R, 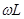 ,
, 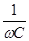 , и частоту
, и частоту 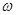 выражать в относительных единицах, для того чтобы коэффициенты полиномов были небольшими.
выражать в относительных единицах, для того чтобы коэффициенты полиномов были небольшими.
Пусть 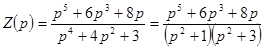 .
.
Знаменатель имеет только мнимые корни  ,
, 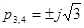 .
.
Поэтому 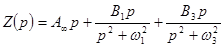 ,
, 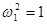 ;
; 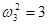 .
.
Кроме того, 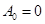 (в этом убеждаемся, положив p = 0 в выражении для
(в этом убеждаемся, положив p = 0 в выражении для 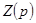 ).
).
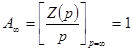 ;
; 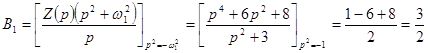 .
.
Аналогично получаем 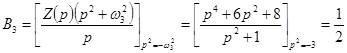
Таким образом, параметры схемы (рис. 6.12), реализуют заданную функцию 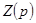 .
.
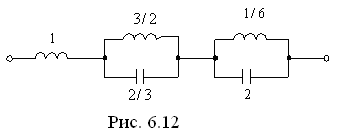 Где
Где 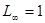 ;
; 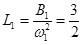 ;
; 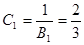 ;
; 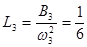 ;
; 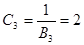 .
.
Рассмотрим теперь операторную проводимость 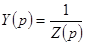
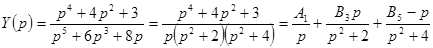 .
.
В данном случае 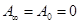 , т.к.
, т.к. 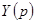 - правильная дробь.
- правильная дробь.
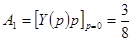 ;
; 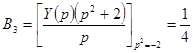 ;
; 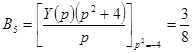
имеем схему, показанную на рис. 6.13,
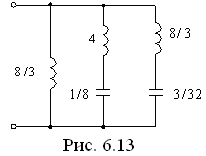 где
где 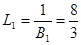 ;
; 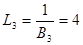 ;
; 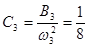 ;
; 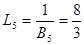 ;
; 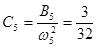 .
.
6.4. Реализация входных функций двухполюсника, имеющих только мнимые корни знаменателя
Если знаменатель входных функций 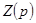 и
и 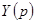 имеет только мнимые корни, то соответствующая цепь состоит только из реактивных элементов. Поэтому в выражении (6.2) должны отсутствовать члены
имеет только мнимые корни, то соответствующая цепь состоит только из реактивных элементов. Поэтому в выражении (6.2) должны отсутствовать члены 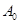 и
и 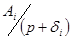 , т.к. при их реализации должны быть использованы активные сопротивления. В соответствии со сказанным
, т.к. при их реализации должны быть использованы активные сопротивления. В соответствии со сказанным 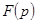 должна иметь вид:
должна иметь вид:
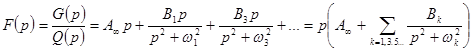 .
.
Отсюда видно, что если все 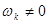 , то
, то 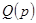 будет полным полиномом от четных степеней
будет полным полиномом от четных степеней 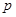 , т.е. полиномом, содержащим все, без пропуска, четные показатели от 0 до “ m ”. При этом
, т.е. полиномом, содержащим все, без пропуска, четные показатели от 0 до “ m ”. При этом 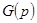 будет полным полиномом нечетных степеней. Учитывая это, запишем
будет полным полиномом нечетных степеней. Учитывая это, запишем
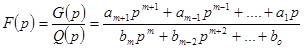 ,
,
где m – четное число.
Значение p = 0 является нулем 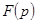 . Если один из корней
. Если один из корней 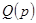 равен нулю, то
равен нулю, то 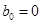 . При этом, сокращая числитель и знаменатель на
. При этом, сокращая числитель и знаменатель на 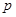 , получим
, получим 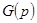 - полином четных степеней,
- полином четных степеней, 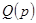 - полином нечетных степеней.
- полином нечетных степеней.
Для возможности реализации 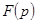 в виде электрической цепи, состоящей из реактивных элементов, необходимо, чтобы она удовлетворяла указанным выше требованиям, а именно: степени полиномов
в виде электрической цепи, состоящей из реактивных элементов, необходимо, чтобы она удовлетворяла указанным выше требованиям, а именно: степени полиномов 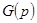 и
и 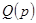 должны отличаться друг от друга на единицу; нули и полюсы
должны отличаться друг от друга на единицу; нули и полюсы 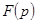 должны чередоваться, т.е.
должны чередоваться, т.е.
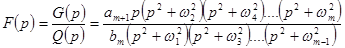 ,
, 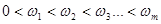 .
.
Если эти условия выполнены, то возможна реализация 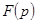 . Существуют различные методы реализации.
. Существуют различные методы реализации.
Метод Фостера заключается в представлении 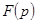 в виде выражения (6.2). Цепи, реализующие каждое слагаемое в (6.2), были рассмотрены выше.
в виде выражения (6.2). Цепи, реализующие каждое слагаемое в (6.2), были рассмотрены выше.
Неудобство метода – необходимость определения корней знаменателя.
В методе Кауэра необходимость в определении корней знаменателя отпадает. Суть этого метода состоит в постепенном выделении частей вида 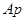 или
или 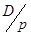 сначала из
сначала из 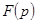 , а затем из остатков после выделения предыдущей части, с последующей реализацией выделяемых частей в виде индуктивной катушки или конденсатора.
, а затем из остатков после выделения предыдущей части, с последующей реализацией выделяемых частей в виде индуктивной катушки или конденсатора.
Пусть 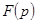 имеет полюс
имеет полюс 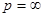 . Это означает, что степень полинома числителя на единицу больше степени полинома знаменателя. Предположим
. Это означает, что степень полинома числителя на единицу больше степени полинома знаменателя. Предположим 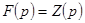 . Разделив числитель и знаменатель, выделяем целую часть
. Разделив числитель и знаменатель, выделяем целую часть 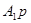 . Получаем
. Получаем
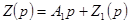 .
.
В 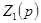 степень полинома в знаменателе на единицу больше. Следовательно, обратная функция
степень полинома в знаменателе на единицу больше. Следовательно, обратная функция 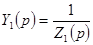 имеет степень числителя на единицу больше степени знаменателя. Следовательно
имеет степень числителя на единицу больше степени знаменателя. Следовательно
 .
.
По аналогии далее получаем 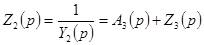 .
.
Эту процедуру продолжаем до тех пор, пока остаток не будет равен нулю. В соответствии с такой операции 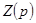 можно представить в виде цепной дроби
можно представить в виде цепной дроби
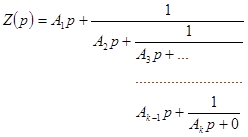 .
.
Отсюда видно, что 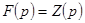 можно реализовать с помощью схемы (рис. 6.14).
можно реализовать с помощью схемы (рис. 6.14).
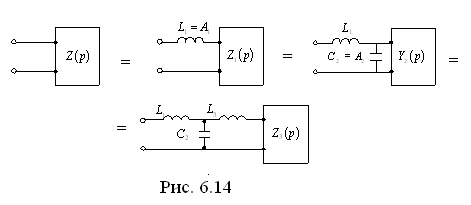
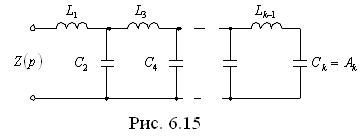
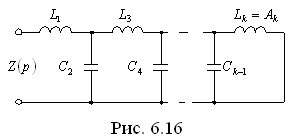
Если k – четное (k – показатель числителя), то цепь будет выглядеть, как показана на рис. 6.15, если k – нечетное, то – как на рис. 6.16.
Если 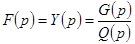 и степень полинома
и степень полинома 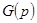 на единицу больше степени полинома
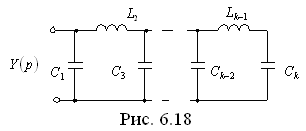
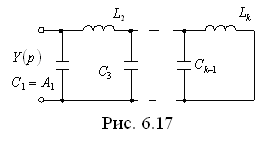
на единицу больше степени полинома 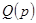 , то, поступая аналогично, получили бы для случая k – четное цепь, показанную на рис. 6.17, или для k – нечетное – цепь, представленную на рис. 6.18.
, то, поступая аналогично, получили бы для случая k – четное цепь, показанную на рис. 6.17, или для k – нечетное – цепь, представленную на рис. 6.18.
Если степень числителя «n» меньше степени знаменателя на единицу, то, добавив в числителе член 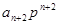 с
с 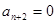 , можно формально пользоваться тем же методом. Однако в данном случае будет
, можно формально пользоваться тем же методом. Однако в данном случае будет 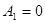 , т.е. в схемах рис. 6.15-6.16 будем иметь
, т.е. в схемах рис. 6.15-6.16 будем иметь 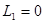 , а в схемах рис. 6.17-6.18
, а в схемах рис. 6.17-6.18 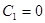 .
.
Рассмотрим теперь случай, когда 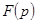 имеет полюс
имеет полюс  . Это означает, что полином знаменателя нечетной степени, а полином числителя четной степени, при этом степень полинома знаменателя на единицу меньше степени полинома числителя. В этом случае постепенно выделяется
. Это означает, что полином знаменателя нечетной степени, а полином числителя четной степени, при этом степень полинома знаменателя на единицу меньше степени полинома числителя. В этом случае постепенно выделяется 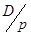 , и получаемая при этом цепная дробь имеет вид:
, и получаемая при этом цепная дробь имеет вид:
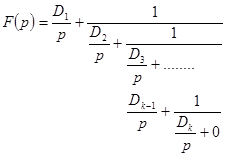 .
.
Пример.
Имеется входная функция цепи 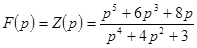 .. Необходимо построить схему цепи.
.. Необходимо построить схему цепи.
Представим функцию цепи в виде 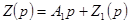 ,
,
где 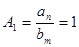 ;
; 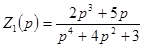 .
.
Найдем проводимость 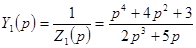 ;
; 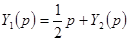 ,
,
где 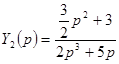 .
.
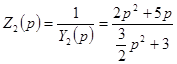 ;
; 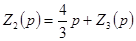 ,
,
где 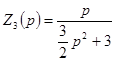 ;
; 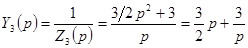 .
.
Таким образом, имеем следующие параметры цепи: 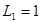 ;
; 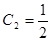 ;
; 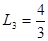 ;
; 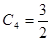 ;
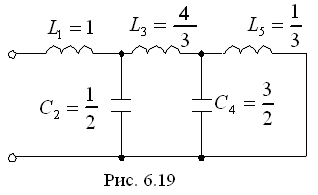
; 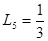 и схему (рис. 6.19)
и схему (рис. 6.19)
6.5. Реализация входной функции, имеющей комплексные
корни
Пусть 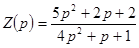 числитель и знаменатель имеют комплексные корни. Для реализации
числитель и знаменатель имеют комплексные корни. Для реализации 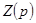 используем метод Бруне. Согласно этому методу приведем
используем метод Бруне. Согласно этому методу приведем 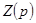 к виду минимального активного сопротивления, т.е. к виду
к виду минимального активного сопротивления, т.е. к виду 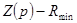 ,где
,где 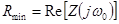
Для определения частоты 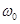 , при которой
, при которой 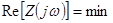 , найдем вещественную часть
, найдем вещественную часть 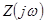 .
.
Вещественная часть 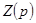 при
при 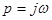 , т.е.
, т.е. 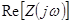 определяется следующим образом. Эта часть, как рациональная дробь, должна иметь члены с четными показателями относительно
определяется следующим образом. Эта часть, как рациональная дробь, должна иметь члены с четными показателями относительно 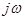 , т.к. только в этом случае при
, т.к. только в этом случае при 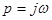 функция будет вещественной. Поэтому представим
функция будет вещественной. Поэтому представим 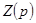 в виде суммы рациональных дробей, состоящих из членов с четными и нечетными показателями.
в виде суммы рациональных дробей, состоящих из членов с четными и нечетными показателями.
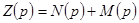 . Так как
. Так как 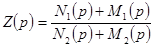 , то, умножив числитель и знаменатель на
, то, умножив числитель и знаменатель на 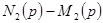 , получим
, получим
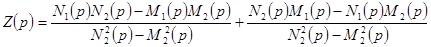 ,
,
где 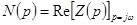 .
.
Согласно этой формуле для рассматриваемого случая имеем
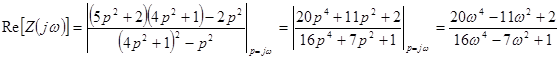 .
.
Возьмем производную и определим экстремумы функции
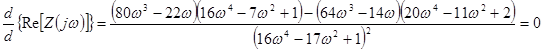 .
.
Отсюда находим 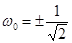 . Этой частоте соответствует
. Этой частоте соответствует 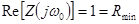 .
.
Таким образом, имеем 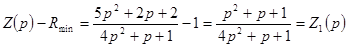 .
.
При 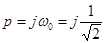 имеем
имеем 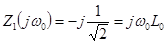 , где
, где 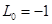 . Тогда
. Тогда 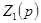 можно представить в виде
можно представить в виде 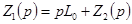 (соответствующая схема цепи показана на рис. 6.20), где
(соответствующая схема цепи показана на рис. 6.20), где 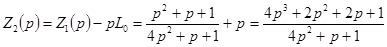 .
.
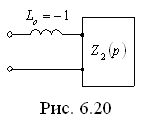 При
При 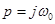 имеем
имеем 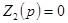 ,
, 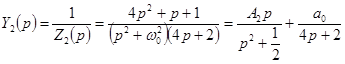 ,
,
где 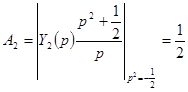 ;
; 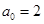 .
.
Поэтому 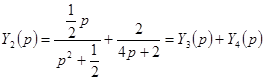 .
.
Реализация 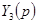 выполняется ранее изложенным методом в виде последовательной цепи из
выполняется ранее изложенным методом в виде последовательной цепи из 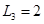 и
и 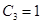 , а реализация
, а реализация 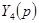 - в виде последовательной цепи из
- в виде последовательной цепи из 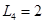 и
и 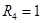 , т.к.
, т.к. 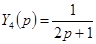 .
.
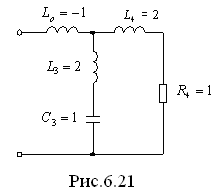 Результирующая цепь, соответствующая входной функции
Результирующая цепь, соответствующая входной функции 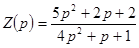 , приведена на рис. 6.21.
, приведена на рис. 6.21.
Отрицательную индуктивность 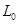 можно реализовать введением в цепь трансформатора с коэффициентом связи
можно реализовать введением в цепь трансформатора с коэффициентом связи 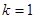 .
.
Date: 2015-09-17; view: 762; Нарушение авторских прав