Расчет сложных цепей постоянного тока методом узловых потенциалов

В методе уравнений Кирхгофа искомыми являются токи в ветвях и соответственно с этим число подлежащих решению уравнений равно числу ветвей, т.е. .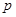

Число решаемых (совместно) уравнений можно уменьшить, если в качестве искомых величин принять потенциалы узлов. Знание этих потенциалов позволяет найти все токи в схеме. Уравнения с узловыми потенциалами (узловые уравнения) вытекают из первого закона Кирхгофа; число этих уравнений равно числу независимых узлов, .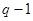

Умножим обе части уравнения

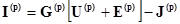
на матрицу 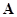и учтем, что 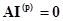. Тогда

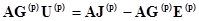. (2.12)

Принимая потенциал узла, для которого отсутствует строка в матрице 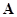, равным нулю, напряжения на ветвях определяем через потенциалы

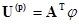. (2.13)

Таким образом, из (2.12) и (2.13) имеем узловые уравнения в матричной форме

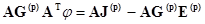. (2.14)

Если обозначить

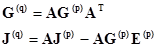, (2.15)

то узловые уравнения будут выглядеть следующим образом

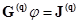, (2.16)

где 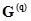- матрица узловых проводимостей, 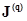- матрица узловых токов. Уравнение (2.16) имеет вид

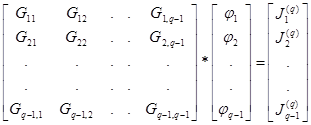. (2.17)

При большом числе узлов уравнение (2.17) решается с помощью компьютера приближенным методом. Если 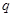- мало, например 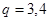, то уравнение (2.17) можно решить аналитически.

Уравнение (2.17) записываем в виде системы алгебраических уравнений

,

, .

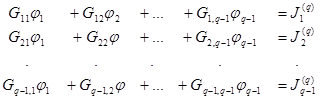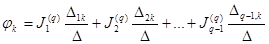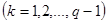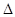- главный определитель системы, 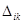- алгебраическое дополнение, полученное вычеркиванием 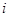-той строки и 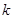-того столбца.

Токи в ветвях определяют по формулам

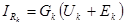или

,

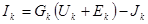где 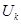выражается через потенциалы узлов.

Пример

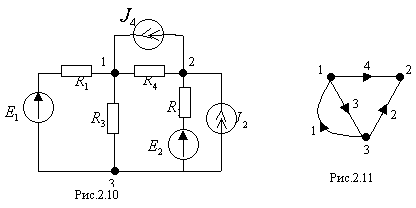
Рассмотрим цепь на рис. 2.10. Она имеет три узла и 4 ветви. Ориентация ветвей на графе (рис. 2.11) схеме выбрана произвольно. Узел 3 берем в качестве базисного (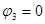). Узловая матрица равна

,

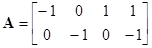а диагональная матрица проводимостей ветвей -

,

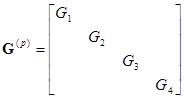где , .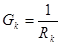

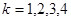Матрица узловых проводимостей

.

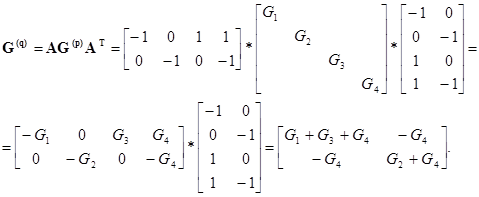Матрица токов источников тока

.

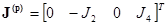Матрица ЭДС источников ЭДС

.

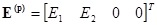Матрица узловых токов

.

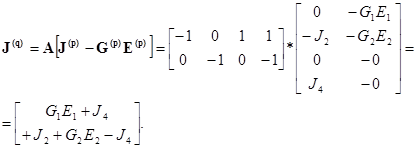Таким образом, узловые уравнения имеют вид

,

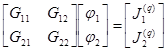где , , , ; , .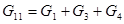

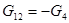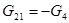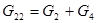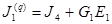Находим токи.

, , ,

.

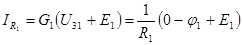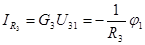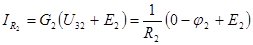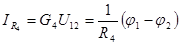
Выводы:

· Матрицы узловых проводимостей 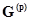имеет порядок . Диагональные элементы этой матрицы (их называют собственными узловыми проводимостями) - это суммы проводимостей (с положительным знаком) ветвей, присоединенных к соответствующему узлу.

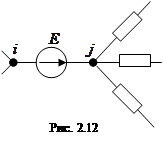· Элемент 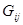матрицы узловых проводимостей (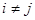) равен сумме проводимостей ветвей, присоединенных между узлам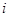и и 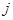, взятой с отрицательным знаком. 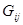(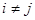) называются общими узловыми проводимостями.

· Матрица 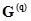симметрична, т.е. 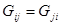и .

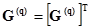· Элемент 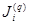матрицы узловых токов равен алгебраической сумме токов источников тока, присоединенных к 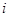-тому узлу, включая токи источников тока, эквивалентные источникам ЭДС. При этом с положительным знаком записывают токи, направленные к узлу.

Знаки элементов всех матриц не зависят от ориентации ветвей графа. Следовательно, узловые уравнения можно составить при непосредственном рассмотрении схемы.

Если в схеме имеются ветви с идеальными источниками ЭДС, то таким ветвям в матрице 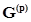соответствует элемент 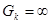. В таком случае схема должна быть преобразована.

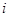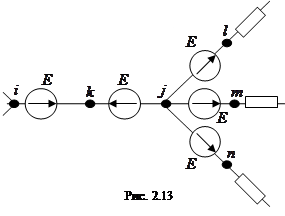
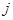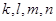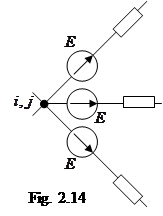
Допустим, что идеальный источник ЭДС включен между узлами и (рис. 2.12). Перейдем к схеме (рис. 2.13), она эквивалентна схеме (рис. 2.12), т. к. потенциалы точек одинаковы относительно узла 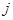в силу чего их можно закоротить. От схемы (рис. 2.13) перейдем к схеме (рис. 2.14). Таким образом, источник ЭДС 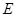можно перенести за узел 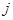, объединив узлы 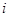и 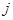. После подобного преобразования можно составить матрицу .

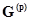Наличие в схеме ветвей с идеальными источниками тока не требует преобразования схемы: в матрице 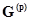таким ветвям соответствуют элементы .

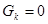Date: 2015-09-17; view: 759; Нарушение авторских прав