
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчет простых цепей постоянного тока
|
|
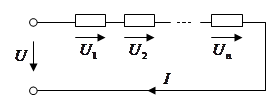 а) Расчет при последовательном соединении участков цепи.
а) Расчет при последовательном соединении участков цепи.
|
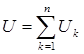 ,
,
т. к. 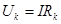 , то
, то
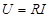 ,
, 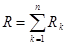 .
.
Таким образом, при последовательном соединении сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Мощность, поступающая в цепь
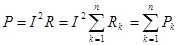 .
.
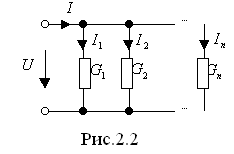 б) Расчет при параллельном соединении участков цепи.
б) Расчет при параллельном соединении участков цепи.
|
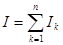 .
.
Но 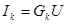 , поэтому
, поэтому
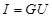 ,
, 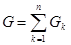 .
.
Таким образом, при параллельном соединении участков проводимость всей цепи равна сумме проводимостей отдельных участков цепи (ветвей).
Мощность, поступающая в цепь
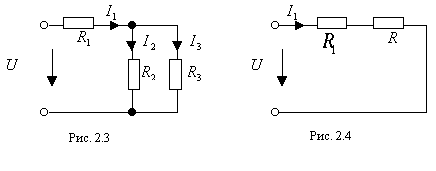
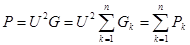 .
.
в) Расчет при смешанном соединении участков цепи (рис. 2.3).
Под смешанным соединением понимается соединение, представляющее сочетание последовательных и параллельных соединений участков цепи. Для расчета таких цепей можно использовать методы, рассмотренные в п.п. а) и б).
Ветви 2 и 3 соединены параллельно. Складывая проводимости этих ветвей, получаем проводимость ветви, эквивалентной указанным двум ветвям
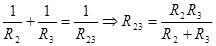 .
.
При этом исходная схема преобразуется в схему из двух последовательно соединенных участков с сопротивлениями 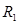 и
и 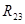 (рис. 2.4)
(рис. 2.4)
 .
.
Возвращаясь к исходной схеме, получаем
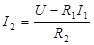 ,
, 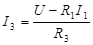
или
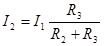 ,
, 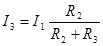 .
.
 |
2.2. Расчет сложных цепей методом уравнений Кирхгофа.
Электрические цепи, схема которых не является простым сочетанием последовательного и параллельного соединений участков цепи, называются сложными цепями.
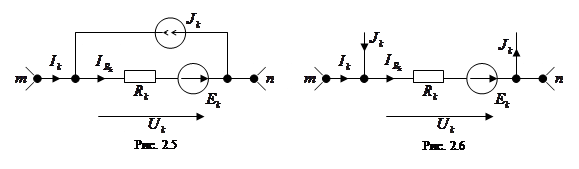
а). Матричная форма закона Ома. Каждая ветвь цепи может содержать сопротивление 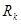 , идеальный источник ЭДС
, идеальный источник ЭДС 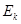 и идеальный источник тока
и идеальный источник тока 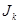 ,
, 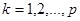 (рис. 2.5). Иногда источники тока не изображают, а показывают только токи источников в соответствующих узлах (рис. 2.6).
(рис. 2.5). Иногда источники тока не изображают, а показывают только токи источников в соответствующих узлах (рис. 2.6).
Ток в сопротивлении 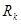
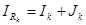 , (2.1),
, (2.1),
где 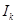 - ток в
- ток в 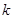 -ой ветви.
-ой ветви.
Для указанных положительных направлений падение напряжения 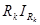 уменьшает, а ЭДС
уменьшает, а ЭДС 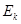 увеличивает потенциал в точке
увеличивает потенциал в точке 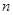 :
:
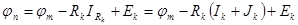 ,
,
т. к. 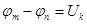 , то
, то
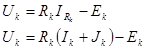 или (2.2)
или (2.2)
отсюда
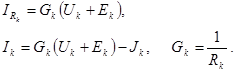 (2.3)
(2.3)
Формулы (2.2) и (2.3) представляют выражение закона Ома для узла цепи с источниками ЭДС и тока.
Если ветвь содержит ряд последовательно соединенных сопротивлений, источников ЭДС и параллельно соединенных источников тока, то в (2.2) и (2.3) вместо 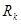 следует понимать суммарное сопротивление, а вместо
следует понимать суммарное сопротивление, а вместо 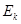 и
и 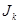 - алгебраическую сумму ЭДС и токов источников. При этом с положительным знаком записывают ЭДС и токи источников, ориентированные относительно
- алгебраическую сумму ЭДС и токов источников. При этом с положительным знаком записывают ЭДС и токи источников, ориентированные относительно 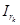 , так как показано на рис. 2.5 (положительные направления
, так как показано на рис. 2.5 (положительные направления 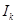 ,
, 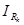 и
и 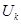 принимают совпадающими и, как правило, указывают одной стрелкой на соответствующей ветви графа).
принимают совпадающими и, как правило, указывают одной стрелкой на соответствующей ветви графа).
Если схема цепи содержит 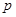 ветвей, то полагая в (2.1)
ветвей, то полагая в (2.1) 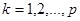 получим
получим 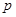 -уравнений, которые можно записать в матричной форме
-уравнений, которые можно записать в матричной форме
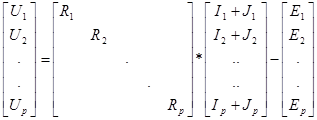
или
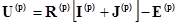 , (2.4)
, (2.4)
где
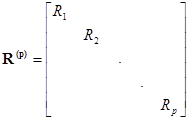 - диагональная матрица сопротивлений ветвей, элемент, находящийся на пересечении
- диагональная матрица сопротивлений ветвей, элемент, находящийся на пересечении 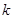 -ой строки и
-ой строки и 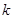 -ого столбца, равен сопротивлению
-ого столбца, равен сопротивлению 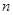 -ой ветви.
-ой ветви.
Аналогично из (2.3) имеем
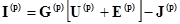 , (2.5)
, (2.5)
где
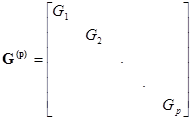 - диагональная матрица проводимостей ветвей. Т.к.
- диагональная матрица проводимостей ветвей. Т.к. 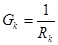 , то матрицы
, то матрицы 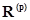 и
и 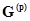 - взаимно обратны, т.е.
- взаимно обратны, т.е.
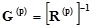 ,
, 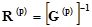 .
.
Формулы (2.4) и (2.5) представляют выражение закона Ома в матричной форме.
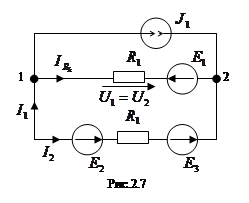 Пример. Используя закон Ома, определить токи на всех участках цепи (рис.2.7). Рассматриваем схему как параллельное соединение двух ветвей, присоединенных к двум узлам (1) и (2). Одна ветвь содержит элементы
Пример. Используя закон Ома, определить токи на всех участках цепи (рис.2.7). Рассматриваем схему как параллельное соединение двух ветвей, присоединенных к двум узлам (1) и (2). Одна ветвь содержит элементы 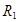 ,
, 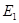 и
и 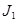 , другая
, другая 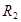 ,
,  и
и 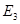 .
.
Для первой ветви имеем
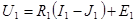 .
.
Для второй ветви
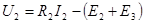 .
.
Т.к. 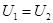 ,
, 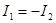 , то
, то
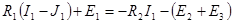 .
.
Отсюда
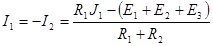 ,
,
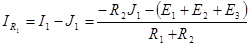 .
.
б). Система уравнений Кирхгофа.
Уравнения, составленные по первому закону Кирхгофа для узлов, имеют вид
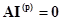 , (2.6)
, (2.6)
где 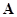 - матрица соединений порядка
- матрица соединений порядка 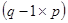 ,
, 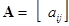 ,
, 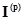 - матрица-столбец токов ветвей (имеет
- матрица-столбец токов ветвей (имеет 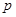 элементов).
элементов).
Уравнения, составленные по первому закону Кирхгофа для сечений
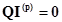 , (2.7)
, (2.7)
где 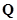 - матрица сечений порядка
- матрица сечений порядка 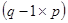 ,
, 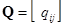 . Матрицы
. Матрицы 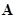 и
и 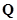 составляются для ориентированного графа схемы. Каждому из уравнений (2.6) или (2.7) соответствует
составляются для ориентированного графа схемы. Каждому из уравнений (2.6) или (2.7) соответствует 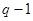 независимых алгебраических уравнений.
независимых алгебраических уравнений.
Уравнения, составленные по второму закону Кирхгофа,
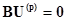 , (2.8)
, (2.8)
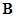 - матрица контуров порядка
- матрица контуров порядка  ,
, 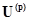 - матрица-столбец напряжений ветвей (имеет
- матрица-столбец напряжений ветвей (имеет 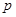 элементов). Уравнению (2.8) соответствуют
элементов). Уравнению (2.8) соответствуют 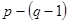 уравнений, которые являются независимыми.
уравнений, которые являются независимыми.
Уравнения (2.6) или (2.7), (2.8) вместе с (2.4) или (2.5) позволяют определить токи 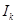 во всех ветвях цепи. Однако целесообразно видоизменять уравнения Кирхгофа. В соответствии с (2.1) запишем
во всех ветвях цепи. Однако целесообразно видоизменять уравнения Кирхгофа. В соответствии с (2.1) запишем
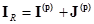 ,
,
где 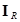 - матрица-столбец (его элемент в
- матрица-столбец (его элемент в 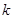 -ой строке
-ой строке 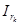 ). Тогда из (2.6) следует
). Тогда из (2.6) следует
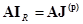 . (2.9)
. (2.9)
Произведение 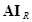 дает матрицу-столбец, элемент
дает матрицу-столбец, элемент 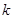 -ой строки этой матрицы равен сумме токов в сопротивлениях ветвей, присоединенных к узлу
-ой строки этой матрицы равен сумме токов в сопротивлениях ветвей, присоединенных к узлу 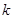 ; при этом с положительным знаком записывают токи, направленные от узла. Произведение
; при этом с положительным знаком записывают токи, направленные от узла. Произведение 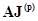 дает матрицу-столбец, элемент
дает матрицу-столбец, элемент 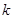 -ой строки этой матрицы равен сумме токов источников тока ветвей, присоединенных к узлу
-ой строки этой матрицы равен сумме токов источников тока ветвей, присоединенных к узлу 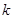 ; при этом с положительным знаком записывают токи, направленные к узлу.
; при этом с положительным знаком записывают токи, направленные к узлу.
Таким образом, (2.9) представляет матричную запись первого закона Кирхгофа. (2.9) соответствуют 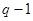 уравнений (независимых).
уравнений (независимых).
Аналогично можно записать и (2.7)
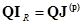 (2.10)
(2.10)
Умножим обе части (2.4) на матрицу 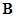 и учтем (2.8), тогда
и учтем (2.8), тогда
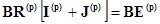 или
или
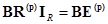 . (2.11)
. (2.11)
 Произведение
Произведение 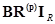 дает матрицу столбец. Элемент
дает матрицу столбец. Элемент 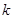 -ой строки равен сумме напряжений на сопротивлениях
-ой строки равен сумме напряжений на сопротивлениях 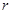 ветвей, из которых состоит контур
ветвей, из которых состоит контур 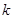 . Произведение
. Произведение 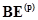 дает матрицу-столбец,
дает матрицу-столбец, 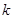 -ый элемент которой равен алгебраической сумме ЭДС
-ый элемент которой равен алгебраической сумме ЭДС 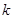 -ого контура. Таким образом, (2.11) представляет матричную запись второго закона Кирхгофа. (2.11) соответствуют
-ого контура. Таким образом, (2.11) представляет матричную запись второго закона Кирхгофа. (2.11) соответствуют 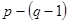 уравнений (которые являются независимыми). Элементы матрицы
уравнений (которые являются независимыми). Элементы матрицы 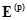 записывают с положительным знаком, если ориентация их тока, как на рис. 2.5.
записывают с положительным знаком, если ориентация их тока, как на рис. 2.5.
Расчет цепи с помощью уравнений Кирхгофа сводится к совместному решению уравнений (2.9) и (2.11) или (2.10) и (2.11). Как правило, искомыми являются токи в сопротивлениях 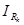 , при известных
, при известных 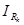 ,
, 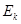 ,
, 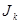 .
.
В схеме цепи могут быть ветви, содержащие только идеальные источники тока или ЭДС. Если уравнения по законам Кирхгофа записываются непосредственно по схеме без применения равенства (2.11), то наличие ветвей с идеальными источниками не вносит никаких изменений.
Если при составлении уравнений по второму закону Кирхгофа применить матричное равенство (2.11), то ветвям, содержащим только идеальные источники тока, соответствуют диагональные элементы 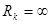 матрицы
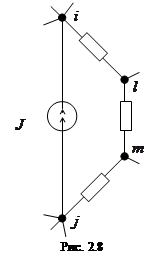
матрицы 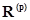 . В этом случае схему необходимо преобразовать. Ветвь с источником тока включена между узлами
. В этом случае схему необходимо преобразовать. Ветвь с источником тока включена между узлами 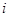 и
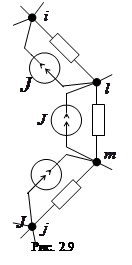
и 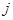 (рис. 2.8). Преобразуем ее к схеме, изображенной на рис. 2.9. Уравнение (2.11) составляют для схемы на рис. 2.9. Следует заметить, что такое преобразование уменьшает число ветвей и контуров схемы.
(рис. 2.8). Преобразуем ее к схеме, изображенной на рис. 2.9. Уравнение (2.11) составляют для схемы на рис. 2.9. Следует заметить, что такое преобразование уменьшает число ветвей и контуров схемы.
Date: 2015-09-17; view: 928; Нарушение авторских прав