
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

В а р и а н т 22
|
|
Частица массой 10 г совершает колебания согласно графику:
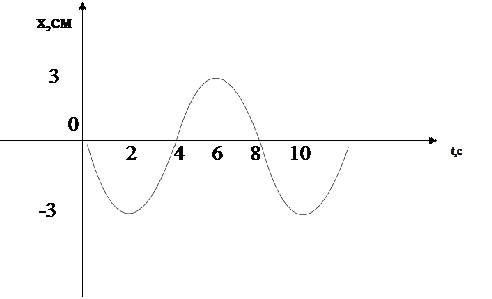 |
Найти в момент времени t = 4 с:
0) величину возвращающей силы;
1) полную энергию;
2) потенциальную энергию;
3) величину максимального ускорения;
4) момент времени, когда модуль ускорения впервые достигает максимума.
Математический маятник (масса шарика 25 г, длина нити
2,4 м) совершает колебания, отклоняясь на угол 50 от вертикали.
Найти:
5) амплитуду колебаний в метрах;
6) циклическую частоту;
7) максимальную скорость шарика;
8) энергию колебаний.
9) Статический прогиб рессоры от груза, положенного на ее середину, равен 2 см. Каким будет наибольший прогиб, когда на середину рессоры упадет тот же груз с высоты 1 м.
| 2,776×10-6 | 1,85×10-2 | 0,2093 | 2,02 | 0,422 | 2,23×10-3 | 0,221 |
В А Р И А Н Т 23
Для частицы массой 5 г график зависимости скорости от времени имеет вид:
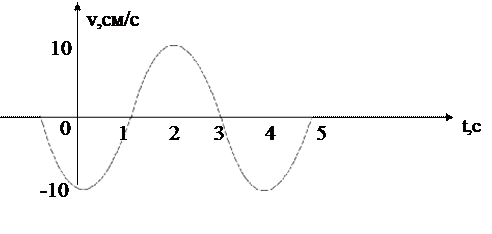 |
Найти:
0) частоту колебаний;
1) амплитуду;
2) начальную фазу в радианах.
Найти также в момент времени t = 4 с:
3) фазу колебаний в градусах;
4) величину возвращающей силы;
5) кинетическую энергию частицы;
6) потенциальную энергию ее.
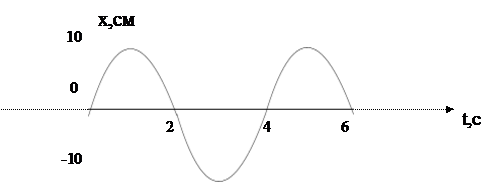 Используя график колебаний маятника, найти:
Используя график колебаний маятника, найти:
 |
7) его максимальную скорость;
8) максимальное ускорение.
Тонкий обруч, подвешенный на гвоздь, вбитый в стену горизонтально, колеблется в плоскости, параллельной стене. Радиус обруча 30 см.
Найти:
9) период колебаний обруча.
| 0,25 | 0,0637 | 3,14 | 2,5×10-5 | 0,157 | 0,2465 | 1,55 |
В А Р И А Н Т 24
Висящий на пружине груз массой 0,1 кг совершает вертикальные гармонические колебания с амплитудой 4 см. Известно, что для упругого удлинения пружины на 1 см требуется сила 0,1 Н. Пренебрегая массой пружины, найти:
0) период колебаний;
1) энергию колебаний.
Точка колеблется гармонически. Амплитуда колебаний равна
5 см, циклическая частота 2 рад/с, начальная фаза равна нулю.
Найти:
2) в какой момент времени скорость точки равна 0,081 м/с?
3) фазу колебаний в этот момент (в градусах);
4) смещение точки от положения равновесия;
5) величину ускорения.
По графику колебаний материальной точки массой 3 г определить:
6) начальную фазу колебаний в радианах;
7) циклическую частоту;
8) величину максимальной возвращающей силы;
9) максимальную кинетическую энергию точки.
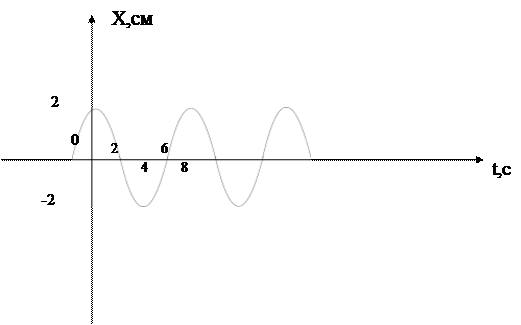 |
| 0,628 | 8×10-3 | 0,314 | 2,939×10-2 | 0,12 | 1,57 | 1,57 | 1,479×10-4 | 1,479×10-6 |
В А Р И А Н Т 25
Математический маятник, колеблющийся с амплитудой 2 см, обладает энергией 9,86×10-6 Дж. Масса маятника 5 г.
Найти:
0) частоту колебаний;
1) длину маятника;
2) максимальную скорость колебаний маятника. (Принять g = p2).
Точка совершает колебания по закону:
Х = 5 × sin 2t (см).
Потенциальная энергия точки впервые от начала колебаний достигла значения 10-4 Дж, а возвращающая сила -5×10-3 Н.
Найти в этот момент:
3) смещение точки от положения равновесия (модуль);
4) фазу колебаний в градусах;
5) ускорение точки (модуль);
6) массу точки;
7) кинетическую энергию точки.
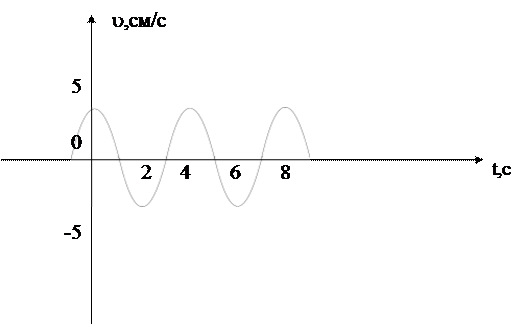
По графику зависимости скорости колебаний точки от времени найти:
8) циклическую частоту;
9) амплитуду колебаний.
 |
| 0,5 | 6,28×10-2 | 0,04 | 0,16 | 3,125×10-2 | 5,647×10-5 | 1,57 | 3,184×10-2 |
В А Р И А Н Т 26
Точка совершает гармонические колебания с амплитудой 5 см и периодом 2 с. Максимальное значение возвращающей силы равно 9,86×10-4 Н.
Найти:
0) массу точки;
1) ее полную энергию;
2) ее максимальную кинетическую энергию.
Используя график зависимости ускорения колеблющейся точки от времени, найти:
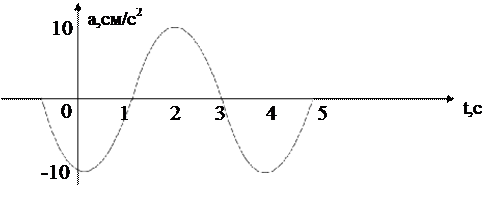 |
3) частоту колебаний.
Найти также в момент времени 2 с:
4) фазу колебаний в радианах;
5) смещение точки от положения равновесия (модуль);
6) скорость точки.
Грузик массой 10 г движется согласно уравнению:
Х = 5 × sin (pt) см.
Найти в момент времени t = 1/6 с:
7) потенциальную энергию грузика;
8) величину возвращающей силы.
Математический маятник массой 10 г, совершающий гармонические колебания с амплитудой 5 см, обладает энергией 4,9×10-5 Дж.
Найти:
9) длину нити маятника.
| 2×10-3 | 2,465×10-5 | 2,465×10-5 | 0,25 | 4,71 | 0,04056 | 3,081×10-5 | 2,465×10-3 | 2,5 |
В А Р И А Н Т 27
На рисунке представлен график зависимости ускорения от времени для частицы массой 5 г.
Найти:
0) циклическую частоту;
1) амплитуду колебаний.
 |
Найти также в момент времени 2 с:
2) величину возвращающей силы;
3) кинетическую энергию частицы;
4) ее потенциальную энергию.
Уравнение движения точки имеет вид:
Х = 3 × sin (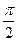 ×t +
×t + 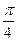 ) см.
) см.
Найти в момент времени t = 0,5 с:
5) фазу колебаний в радианах;
6) скорость точки;
7) величину ускорения.
Тонкий обруч, подвешенный на гвоздь, вбитый в стену горизонтально, колеблется в плоскости, параллельной стене. Радиус обруча 30 см.
Найти:
8) период колебаний обруча;
9) частоту колебаний.
| 1,57 | 4,056×10-2 | 5×10-4 | 1,014×10-5 | 1,57 | 7,395×10-2 | 1,55 | 0,645 |
Date: 2015-09-17; view: 2421; Нарушение авторских прав