
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Закрепление материала по контрольным вопросам и тестам
|
|
Абсолютные величины в медицине дают большую информацию о размере, силе явления или признаков. Например, возраст, рост, вес, величина кровяного давления человека и т.д. Однако во многих случаях абсолютная величина не показывает размер, силу явления или признака. Абсолютные величины являются мало пригодными для сравнения их с другими величинами, характеризующими явления. Они нужны только как промежуточная стадия для получения относительных показателей.
Например, в городе А. заболело 2000 детей, а в городе Б. – 1500. Это не означает, что в городе А. болеют чаще, чем в городе Б. Для того, чтобы определить размер явления, необходимо учитывать различия в численности населения данных городов, т.е. учесть величину среды (численность детей), в которой происходит явление (число больных). Численность детей в городе А. равно 8000 человек, а в городе Б. – 3000. Отсюда, несмотря на большее число больных в городе А., они составляют около четверти всего количества детей (2000:8000). А в городе Б. при меньшем числе больных они составляют половину количества детей (1500:3000). Таким образом, во многих случаях сравнивают не абсолютные величины, а так называемые относительные величины.
Относительные величины – это результат сравнения (отношения, деления) двух абсолютных величин.
Виды относительных величин:
· интенсивные;
· экстенсивный (структуры);
· координации;
· правдоподобия;
· соотношения;
· наглядности.
Интенсивные показатели характеризуют распространение или частоту изучаемого явления или признака в среде. (Например, численность населения в г. Н (величина среды, в которой происходит явление) – 5000, число больных (размер явления) – 250). Интенсивный показатель отвечает на вопрос: «как часто явление встречается в среде?».
Методика вычисления:
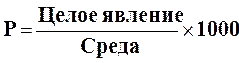
P – интенсивный показатель
Целое явление – количество больных
Среда – численность населения
1. Составление пропорции:
Численность населения – число больных 5000 – 250
1000 – х 1000 – х
2. Вычисление показателя:
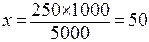 ‰ (или 50 больных на 1000 населения)
‰ (или 50 больных на 1000 населения)
Вывод: в городе Н.на 1000 населения приходится 50 больных (50‰)
Величина основания интенсивных показателей
За величину основания обычно выбирают – 100, 1000, 10000, 100000 (при вычислении рождаемости, смертности, естественного прироста населения, общей заболеваемости - за основание обычно принимают 1000 чел. населения; вычисление размеров смертности или заболеваемости в отношении какой либо отдельной болезни или группы болезней производится на 10 000 или 100 000 населения, вычисление показателей временной нетрудоспособности в связи с заболеваниями производится на 100 работающих). Материнская смертность вычисляется на 100 000 рожденных живыми. Соответственно, коэффициент интенсивности выражается в процентах – 100 (%), промилле – 1000 (‰), продецимилле – 10000 (‰о), просантимилле – 100000 (‰оо).
Показатель лучше обозначать не математическими знаками (‰о), а цифрами – на 10000, 100000 населения.
Экстенсивный показатель характеризует состав или структуру явления, соотношение размеров частей явления к целому (показывает долю или удельный вес). Экстенсивный показатель отвечает на вопрос: «какая часть?». Экстенсивный показатель показывает, как распределяется изучаемое явление на свои составные части, каков удельный вес данного явления по отношению ко всей его величине (отношение части к целому). (Например, число заболеваний (целое явление)) – 250, из них больных с заболеванием органов дыхания (часть целого) – 125.
Методика вычисления:
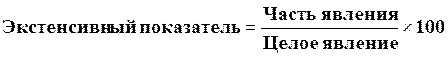
Часть явления – больные с заболеванием органов дыхания
Целое явление – общее количество заболеваний
1. Составление пропорции.
Целое явление – часть явления 250 – 125
100 – х 100 – х
2. Вычисление показателя.
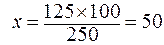 %.
%.
Вывод: из всего количество заболеваний удельный вес больных с заболеванием органов дыхания составляет 50%.
Для вычисления экстенсивного показателя величину основания принимают за 100 и выражают в процентах – 100 (%).
При вычислении нескольких экстенсивных показателей, сумма всех показателей обязательно должна быть равной 100 (Например, болезни органов дыхания составляют – 50%, инфекционные и паразитарные – 25%, болезни мочеполовой системы – 25%).
Различия между интенсивным и экстенсивным показателями
(эти два показателя по своему содержанию значительно отличаются)
| Интенсивный показатель | Экстенсивный показатель |
| 1. Сравнивают между собой | 1. Не сравнивают, или сравнивают с большой осторожностью, глубоко зная сущность сравниваемых явлений |
| 2. Необходимо иметь среду (численность населения) и явление, произошедшее в данной среде (число больных определенным заболеванием). | 2. Надо иметь целое явление (общее число заболеваний) без среды и часть его (число заболеваний определенной нозологии). |
| 3. С изменением среды изменяется явление | С изменением целого явления его часть может, не изменяться. |
| 4. Явление связано со средой. | Явление не связано со средой. |
| 5. Отвечает на вопрос: «Как часто?» | Отвечает на вопрос: «Какая часть?» |
Примечание: экстенсивный показатель нельзя применять для установления динамики изучаемого явления во времени или для сравнения степени его распространения в двух или нескольких группах населения.
Показатели координации характеризует соотношение частей целого между собой. Например, в городе Н число врачей 200, число средних медицинских работников – 600.
Методика вычисления:
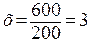
Вывод: соответствие врачей и средних медицинских работников относится как 1:3, т.е. на 1 врача приходится 3 средних мед. работников.
Коэффициенты правдоподобия – это числовые соотношения одноименных показателей структуры, рассчитанные на двух разных совокупностях. В таблице 3.1 в графе 6 приведены коэффициенты правдоподобия, когда показатели структуры г. А делятся на показатели структуры в г. Б.
Таблица 3.1
Date: 2015-09-17; view: 582; Нарушение авторских прав