
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Стохастическая сетевая модель. Граф передач и матрица вероятностей передач
|
|
Модель вычислительной системы может быть представлена как совокупность рассмотренных СМО, которые отображают отдельные устройства или группы однотипных устройств, а также связи между устройствами. Совокупность взаимосвязанных СМО называется стохастической сетевой моделью.
В конфигурации стохастической сети отражаются:
а) структура вычислительной системы;
б) последовательность выполняемых вычислительных этапов обработки информации.
Для простейших сетей в теории массового обслуживания принято:
а) входной поток l является простейшим;
б) длительность обслуживания n подчиняется экспоненциальному закону (если отсутствуют сведения о законе распределения длительности обслуживания):
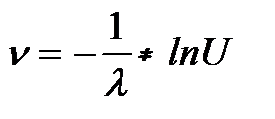 ,
,
где U – поток равномерно распределенных случайных величин. На основе конфигурации стохастической модели формируются аналитические выражения, по которым непосредственно могут быть оценены характеристики системы.
В качестве примера рассмотрим следующую вычислительную систему (рис.1.8), в которую входят следующие подсистемы: S1 - процессор; S2 – быстродействующее ВУ (например, накопитель на магнитных дисках (НМД)); S3 – быстродействующее ВУ (например, накопитель на магнитных лентах (НМЛ)); S4 - группа однотипных медленно действующих ВУ(например, принтеры); S5 - канал передачи данных.

Рис. 1.8
В такой стохастической сети предполагается, что отсутствует последействие. Это означает, что все последующие события могут зависеть только от текущего события и не зависят от предшествующих событий. Такой процесс называется марковским. Он характеризуется множеством состояний S1... S5 и матрицей вероятностей перехода в эти состояния. Вычислительный процесс всегда начинается с момента поступления заявки в процессор (состояние S1). Инициализация обращения к любому из устройств осуществляется только процессором. Связи между отдельными СМО устанавливаются в результате анализа порядка следования этапов обработки заявок. Для отображения вычислительного процесса используется направленный граф передач. Вершины графа соответствуют состояниям вычислительного процесса S1, S2, … Sn, а дуги между вершинами указывают на связи между отдельными СМО (переход системы из одного состояния в другое). Дуги взвешиваются вероятностями перехода. Если система может перейти из одного состояния в одно из нескольких состояний, то возникает необходимость оценки вероятностей переходов. При этом строится матрица вероятностей передач.
Этап – процесс, завершающийся выходом заявки из процессора.
| P01 |
| P51 |
| P13 |
| P35 |
| P10 |
| P12 |
| P14 |
| P41 |
| P25 |
| l |
| l |
| S2 |
| S4 |
| S5 |
| S1 |
| S3 |
| S0 |
Рис. 1.9
Граф вероятностей передач и матрица вероятностей передач представлены на рис. 1.10.
| S0 |
| S1 |
| S2 |
| S3 |
| S4 |
| S5 |
| P01 |
| P51 |
| P13 |
| P35 |
| P10 |
| P12 |
| P14 |
| P41 |
| P25 |
| S0 S1 S2 S3 S4 S5 S0 P00 P01 P02 P03 P04 P05 S1 P10 P11 P12 P13 P14 P15 S2 P20 P21 P22 P23 P24 P25 S3 P30 P31 P32 P33 P34 P35 S4 P40 P41 P42 P43 P44 P45 S5 P50 P51 P52 P53 P54 P55 |
Рис. 1.10
Здесь указаны вероятности перехода p ji из j -ой подсистемы в i -ю. S0 - источник заявок (генератор заявок) в системе. Таким образам, число подсистем в системе (n+1 ), и размерность матрицы вероятностей передач соответственно тоже (n+1 ).
Рассмотрим, как оценивается вероятность перехода p ji из j -ой подсистемы в i -ю. Для этого возьмём две вершины графа Sj и Si (рис.1.11) и тогда pji можно определить в виде
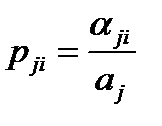 ,
,
где 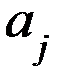 - весь суммарный (средний) поток, который исходит из подсистемы Sj;
- весь суммарный (средний) поток, который исходит из подсистемы Sj; 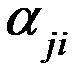 - средний поток заявок, который из подсистемы Sj поступает в Si; входной и выходной потоки равны.
- средний поток заявок, который из подсистемы Sj поступает в Si; входной и выходной потоки равны.
Sj
pji
i Si
Рис.1.11
Рассмотрим простейший пример расчета для системы на рис.1.9. Пусть S2 и S3 - внешние накопители. Имеется N файлов, которые распределены между накопителями S2 и S3. К каждому файлу при решении средней задачи должно быть осуществлено Dj обращений (j = 1, N). При каждом полном решении задачи на выходе системы появляется обслуженный запрос, который направляется к S0. Пусть также к внешнему устройству S4 при обслуживании средней задачи осуществляется d обращений.
Общее количество обращений к файлам D определяется в виде
D = 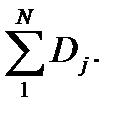
На выходе S1 заявка появляется (D + d + 1) раз.
Матрица вероятностей передач имеет вид, представленный на рис. 1.12.
| S0 S1 S2 S3 S4 S5 S0 0 P01 0 0 0 0 S1 P10 0 P12 P13 P14 0 S2 0 0 0 0 0 P25 S3 0 0 0 0 0 P35 S4 0 P41 0 0 0 0 S5 0 P51 0 0 0 0 |
Рис.1.12.
Значения вероятностей передач определяются в следующем виде:
P01 = 1; P25 = 1; P35 = 1; P51 = 1; P41 = 1;
P10 = 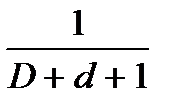 ; P14 =
; P14 = 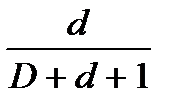 ; P12 =
; P12 = 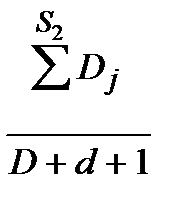 ; P13 =
; P13 = 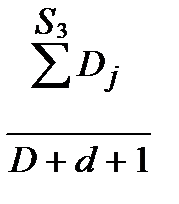 .
.
Суммы вероятностей передач по строкам должны удовлетворять соотношению
P10 + P12+P13+P14 =1.
§1.6. Разомкнутые и замкнутые стохастические сети. Параметры стохастических сетей
Для описания вычислительных систем используют следующие понятия:
а) разомкнутые стохастические сети (информационные системы оперативной обработки запросов, продажа железнодорожных билетов и т.п.);
б) замкнутые стохастические сети (работа вычислительной системы в многозадачном (пакетном) режиме). Эти системы не имеют чётко определённого входного потока запросов l; в данном случае источник запросов представляется как фиктивный в связи между выходом и входом.
| Разомкнутая |
| С |
| l |
| Замкнутая |
| С |
| l |
Рис. 1.16
Параметры стохастических сетей (исходные данные для расчёта исследуемой вычислительной системы):
1. Число СМО (S1, S2,..., Sn) - (n + 1).
2. Число каналов K1, K2,..., Kn в подсистемах S1, S2,..., Sn.
3. Матрица вероятностей передач P = [ pji ]; 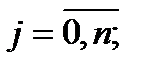
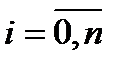 .
.
4. l0 - средняя интенсивность источника заявок для разомкнутых сетей.
5. M - коэффициент многозадачности для замкнутых сетей.
6. n1, n2,..., nn - длительности обслуживания, характеризующие задержки в подсистемах S1, S2,..., Sn.
Date: 2015-09-05; view: 618; Нарушение авторских прав