Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Использование для выравнивания распределения опытной информации закона распределения Вейбулла
|
|
Дифференциальную функцию или функцию плотностей вероятностей ЗРВ описывают уравнение
,
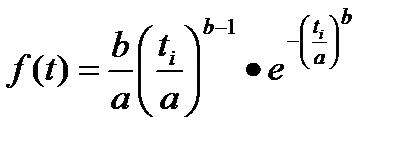где a,b – параметры ЗРВ.
Параметр b определяют по таблице 3. Из таблицы выписывают параметр b коэффициенты kb и cb , предварительно посчитав коэффициент вариации.
При V =0,54; b = 1,9; kb =0,89; С b =0,49.
Параметр a рассчитывают по одному из уравнений
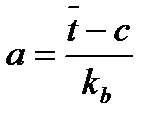или 
,
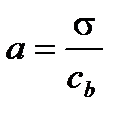Отсюда получаем
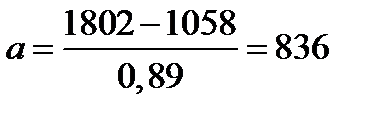мото-ч
Дифференциальную функцию при ЗРВ определяют по таблице 5, используя уравнение
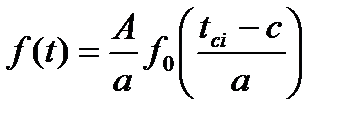
где А – длина интервала статистического ряда;
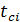- середина интервала статистического ряда;
С – смещение начала рассеяния.
Рассчитаем значения функции во всех интервалах статистического ряда
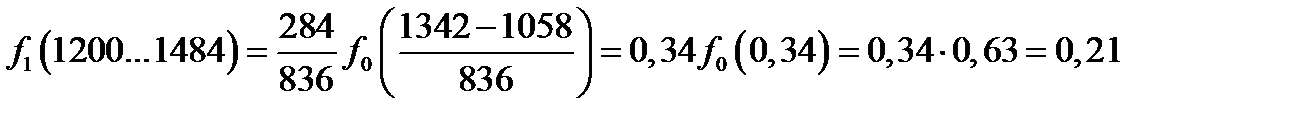
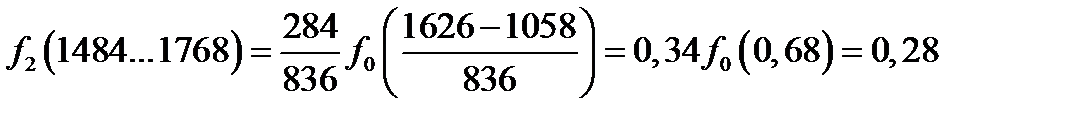
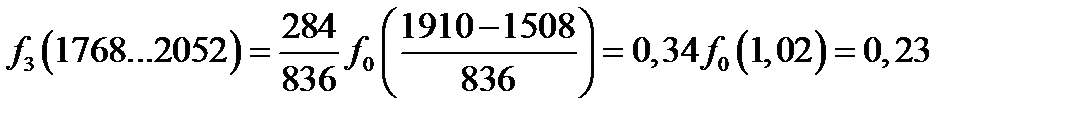
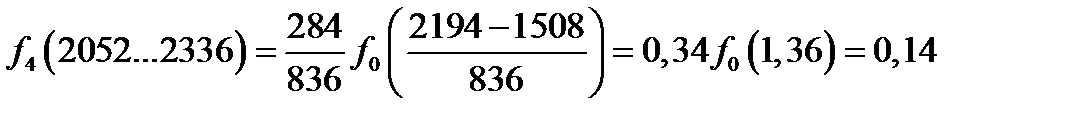
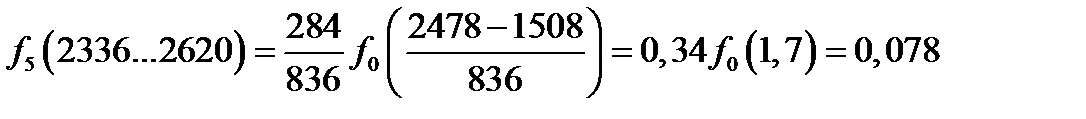
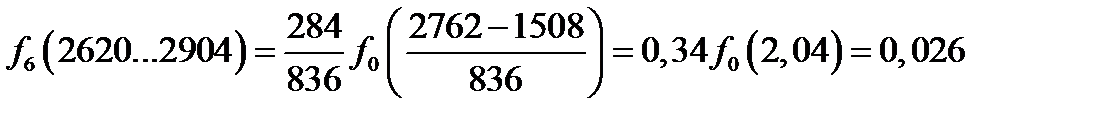
Интегральную функцию или функцию ЗРВ определяют по уравнению
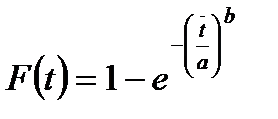
Интегральная функция приведена в таблице 6. При этом используют уравнение
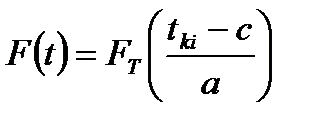
Определяем значения интегральной функции во всех интервалах статистического ряда
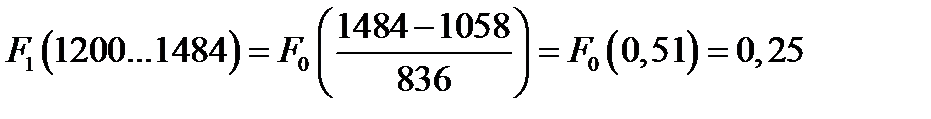
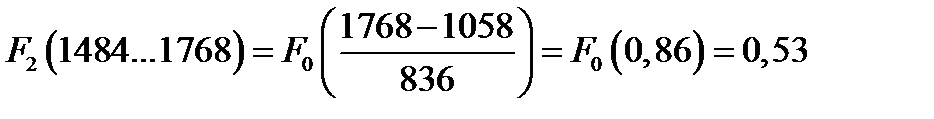
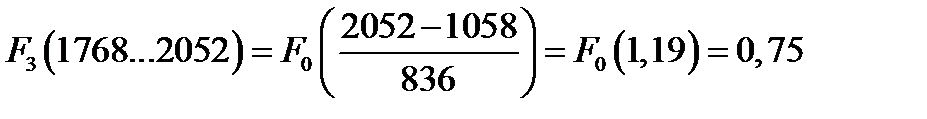
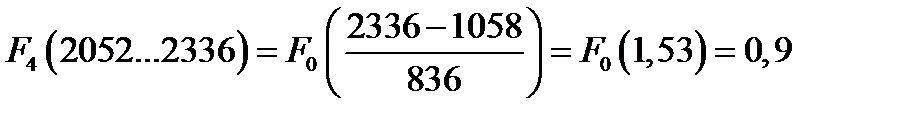
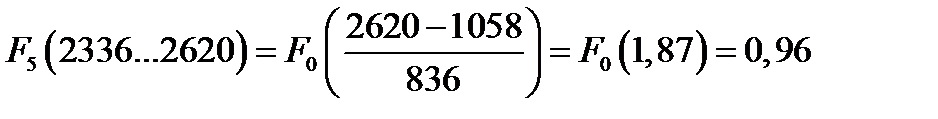
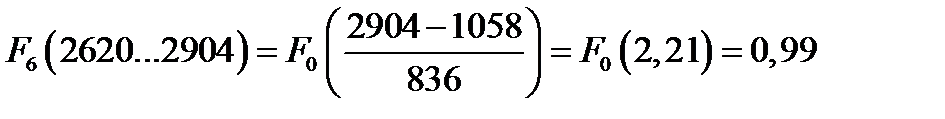
Рассчитанные значения функций сводим в таблицу
1.4 Таблица - Значения дифференциальной и интегральной функций при ЗРВ
| Интервал мотто-ч | 1200-1484 | 1484-1768 | 1768-2052 | 2052-2336 | 2336-2620 | 2620-2904 |
| f(t) | 0,21 | 0,28 | 0,23 | 0,14 | 0,078 | 0,026 |
| F(t) | 0,25 | 0,53 | 0,75 | 0,9 | 0,96 | 0,99 |
На основании полученных значений f(t) и F(t) могут быть построен графики дифференциальных и интегральных функций закона распределения Вейбулла.
При построении дифференциальной кривой (рисунок 6) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значение дифференциальной функции. Точки пересечения образуются значением дифференциальной функции по сои ординат и значением середины i-го интервала по оси абсцисс.
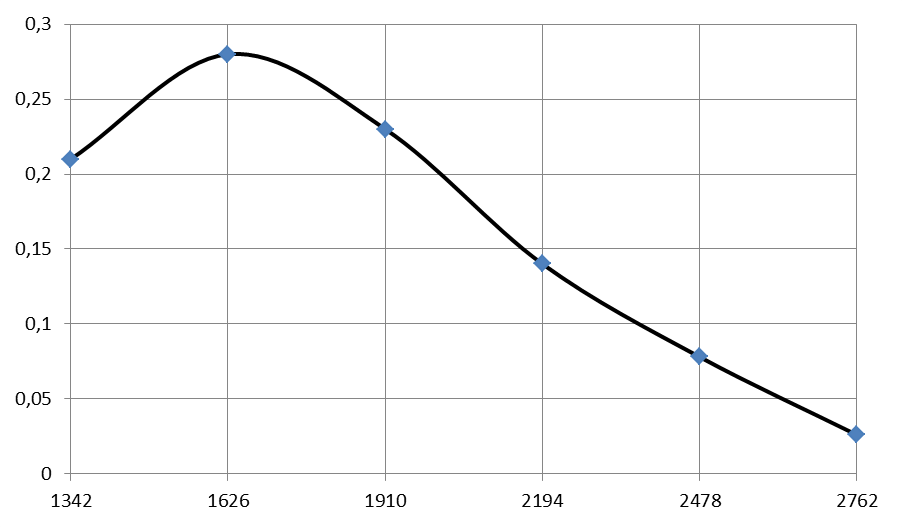
Рисунок 6. Дифференциальная кривая
При построении интегральной кривой (рисунок 7) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значением интегральной функции.
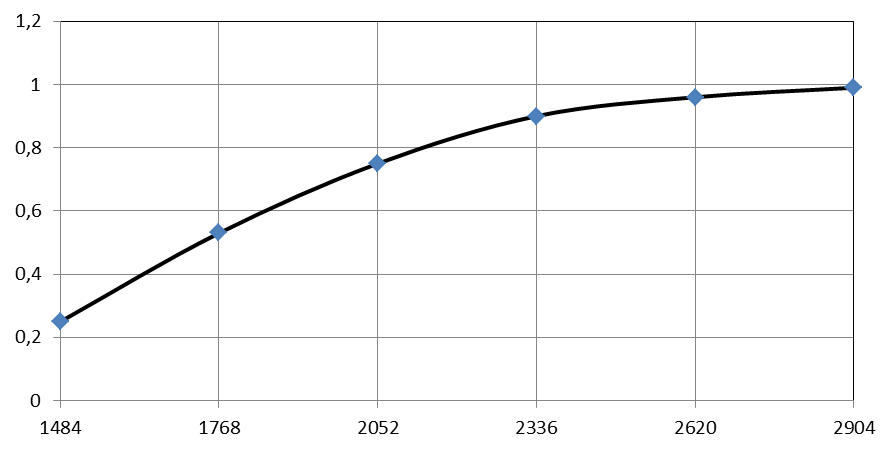
Рисунок 7. Интегральная кривая
Определим число двигателей, потребующих ремонта в интервале наработки от 1700 – 2200 мото-ч.
Решение:
- по дифференциальной функции:
.
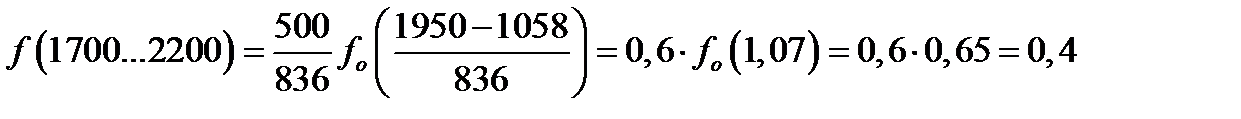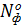= 0,4∙29≈ 12 двиг.
- по интегральной функции
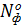= 0,38∙29≈ 12 двиг.
Date: 2015-09-05; view: 584; Нарушение авторских прав