Линии тока и траектории. Функции тока

В гидродинамике обычно одну из лагранжевых координат, например L₁, связывают с функцией тока Ψ, совпадающей с L₁ с точностью до постоянного сомножителя и несущественной аддитивной константы:

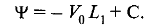(1.2.103)

Тогда из 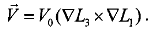(1.2.102) с учетом (1.2.103) получим

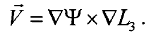(1.2.104)

В частности, при двухмерном течении, когда L₃ = Е₃, из (1.2.104) имеем

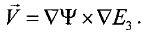(1.2.105)

Из теории векторных полей известно, что векторной линией называется пространственная линия, в каждой точке которой касательная к ней совпадает с направлением вектора в этой точке. Векторная линия поля скоростей называется линией тока. Касательная к этой линии – весктор скорости.

Совокупность всех векторных линий образует картину течения в данный момент времени. Следовательно, элемент длины d 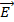линии тока колинеарен вектору скорости 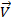: 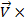d 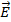= 0. Отсюда, имеем

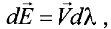(1.2.106)

где dλ - скалярный параметр. В скалярной форме (1.2.106) имеет вид

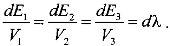(1.2.107)

Эти соотношения называются дифференциальным уравнением линии тока.

Подобно соотношению 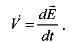(1.2.15) уравнения (1.2.106), (1.2.107) представим в виде

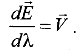(1.2.108)

Отличие (1.2.15) и (1.2.108) состоит в том, что в (1.2.15) время t входит как в левую, так и в правую части равенства, а в (1.2.108) - только в правую часть.

Интегрирование (1.2.15) по времени позволяет рассчитать траекторию движения материальной частицы - линию, по которой перемещается эта частица. (Траектория материальной частицы - кривая, которую описывает частица во время движения. При стационарном процессе совпадает с линией тока.) Таким образом, в общем случае линия тока и траектория материальной частицы не совпадают. Для стационарных полей скоростей 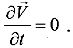(1.2.24) время как переменная величина не входит в первую часть соотношения (1.2.15). Поэтому для стационарных течений скалярные параметры dt в (1.2.15) и dλ в (1.2.106) - (1.2.108) практически совпадают, что для таких течений приводит к совпадению понятий «траектория материальной частицы» и «линия тока».

Покажем, что в стационарных течениях на линии тока величины Ψ и L₃, входящие в (1.2.104), постоянны. Для этого подставим (1.2.104) в дифференциальное уравнение линии тока (1.2.107).

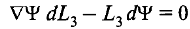(1.2.109)

Обращение (1.2.109) в тождество может быть связано либо с равенством нулю дифференциалов Ψ и L₃

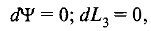(1.2.110)

либо с пропорциональностью Ψ и L3. Последнее невозможно, так как в соответствии с (1.2.103) функция Ψ пропорциональна лагранжевой координате L₁, и вследствие линейной независимости всех координат L_i функция Ψ не может быть пропорциональна двум другим лагранжевым координатам, в том числе и L₃. Следовательно, (1.2.110) является единственным условием обращения (1.2.109) в тождество. Так как условия (1.2.110) выполняются вдоль линии тока, то это значит, что на этой линии имеем Ψ= const и L₃ =const, а сама линия тока находится на пересечении изоповерхностей 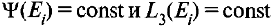(рис. 17).

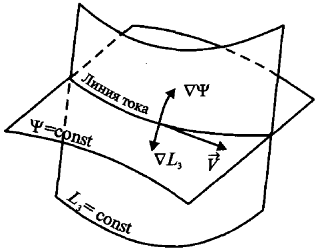
Рис. 17. Линия тока как пересечение поверхности тока Ψ = const с лаrpанжевой

поверхностью L_з = const

Изоповерхность Ψ = const называется поверхностью тока. Таким образом, функцией тока

называют всякую функцию 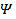типа (1.2.103), принимающую на линии и поверхности тока

постоянное значение. (Функция тока – скалярная величина, которая задает течение среды.)

Date: 2015-09-05; view: 679; Нарушение авторских прав