Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Поле вектора скоростей. Стационарное и нестационарное поле скоростей
|
|
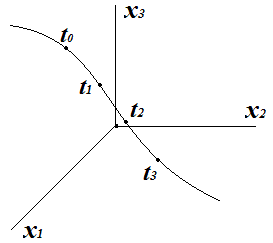
Поле вектора скорости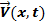 
описывает мгновенную картину течения всей совокупности материальных частиц
П о определению изменение пространственных координат материальных частиц по времени называется скоростью перемещения частиц (в дальнейшем – скоростью) и вычисляется по формуле (1.2.15).
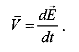(1.2.15)
Вектор скорости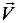 
можно так-же рассчитать по формуле
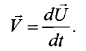(1.2.90)
В лагранжевых координатах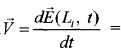 
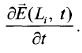
В эйлеровых координатах вследствие независимости пространственных координат от времени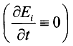 
такая процедура приводит к тождеству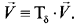 
На практике наибольший интерес представляет раскрытие полной производной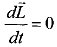 
(1.2.10) с помощью 
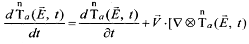(1.2.16), где вместо 
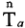нужно подставить 
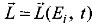(1.2.9):
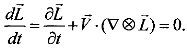(1.2.91)
Отсюда, решая замкнутую относительно компонент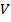 
i вектора скорости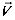 
систему, приходим к формуле И. И. Гольденблата
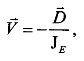(1.2.92)
где компоненты Di вспомогательного вектора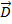 
получаются из якобиана преобразования эйлеровых координат в лагранжевы 
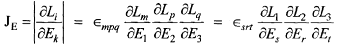(1.2.20) путем замены дифференцирования лагранжевых координат по координате Ei дифференцированием по времени t. Если такую замену дифференцирования выполнить в декартовых координатах, то компоненты вспомогательного вектора будут иметь вид
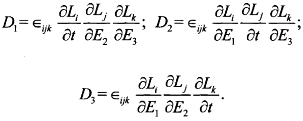(1.2.93)
Для произвольных координат вспомогательный вектор
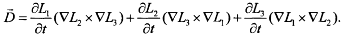(1.2.94)
Подстановкой (1.2.94) в (1.2.92) получим окончательный вид формулы, предложенной в кинематике Б. В. Кучерневым, для определения вектора скорости по заданному закону движения 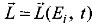(1.2.9) в эйлеровых координатах:
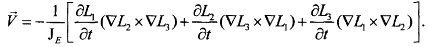(1.2.95)
в общем случае
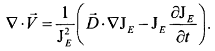(1.2.97)
в частном случае при выполнении условия постоянства объема в пространственных координатах JE=1 (1.2.55) устанавливаем, что в окрестности мaтeриальной частицы, движущейся без изменения объема, поле скоростей должно быть соленоидальным:
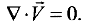(1.2.98)
это соотношение называется условием несжи.маемосmи сплошной среды. Выполнение условия постоянства объема (1.2.55) приводит (1.2.92) к виду
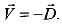(1.2.99)
в частности, в декартовых прямоугольных координатах такой вектор имеет компоненты, совпадающие с точностью до знака с компонентами вектора 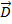в формуле (1.2.93).
Принятые допущения, гипотезы, определения и их следствия позволяют рассматривать реальный мир как объект математического моделирования. Оставляя, как оговорено выше, за собой возможность при необходимости расширять конечную совокупность свойств Р объекта исследования М, можно создавать модели в идеализированном пространстве, сколь угодно близкие к поведению материи в реальном пространстве и времени.
Естественно, что вечное движение материи исследователь изучает лишь в определенном временном интервале. Если исследуемая конечная совокупность свойств Р материального объекта не претерпевает значимого изменения в рассматриваемом интервале времени, то утверждают, что объект участвует в стационарном nроцессе движения. Для нестационарных nроцессов значимым является начальное состояние (в начальный момент времени to исследования) объекта. Для таких процессов это состояние должно быть задано начальными условиями (начальными при t = to значениями всех исследуемых свойств объекта).
Стационарный процесс. Независимость процесса движения от времени t в лагранжевом и эйлеровом множествах отсчета имеет различную физическую трактовку. Пусть количественной характеристикой некоторых свойств сплошной среды является тензор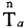 
.
В любом множестве отсчета процесс изменения этой величины называется стациoнapным, если
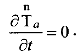(1.2.23)
для лагранжевых координат из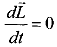 
(1.2.10) следует, что записи (1.2.23) эквивалентна запись 
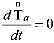. Физический смысл этого состоит в том, что характеристика свойств 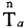окрестности одной и той же частицы т при ее прохождении через различные пространственные точки п не меняется.
Для эйлеровых координат из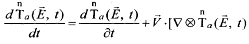 
(1.2.16) следует, что записи (1.2.23) эквивалентна запись 
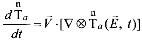. Физический смысл этого состоит в том, что характеристика свойств окрестности частицы т полностью определяется координатами Еi пространственных точек п и значением вектора скорости 
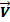материальных частиц в этих точках. Иными словами, в фиксированной пространственной точке п для любой материальной частицы т, попадающей в положение п, характеристика свойств не меняется. В частности, для стационарного поля скоростей
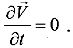(1.2.24)
В заключение отметим, что окончательный вид приведенных полей скоростей, которые могут быть использованы для моделирования процессов ОМД, определяется видом функций, описывающих значения текущих размеров и формы деформируемой заготовки. В наиболее простом виде такие функции учитывают основные геометрические характеристики области течения металла. Соответствующие таким функциям поля скоростей рекомендуется использовать как основное
решение, последующая корректировка которого позволяет кроме геометрических параметров исследуемого процесса ОМД учитывать реологическое поведение деформируемого металла. Моделирования процесса прокатки в условиях плоской деформации с аппроксимацией изменения текущей высоты h полосы по произвольному закону, например по окружности, может быть использовано векторное поле.
В общем случае вид поля скоростей, соответствующий решению исследуемой задачи ОМД, определяется полнотой выполнения требований, оговоренных в постановке задачи. Поле скоростей, удовлетворяющее всем требованиям постановки краевой задачи, будем называть реальным (действительным) полем (Р - полем) скоростей. Как правило, Р-поля скоростей удается построить лишь в отдельных случаях. Чаще всего решение задачи сводится к поиску наилучшего приближения к Р-полю. Среди всех векторных полей, во множество которых обязательно входят р- поля скоростей, выделим поля скоростей, удовлетворяющие кинематическим краевым условиям (для стационарных течений - кинематическим граничным условиям). Такие поля будем называть кинематически возможными полями (КВ-полями) скоростей.
Для КВ-полей скоростей на некоторых поверхностях допускается разрыв (скачок) вектора скорости за счет тангенциальной к этим поверхностям составляющей вектора скорости. Такие поля будем называть разрывными КВ-полями скоростей.
Date: 2015-09-05; view: 1222; Нарушение авторских прав