Основные операции производимые над векторами

Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c -- его диагональю (рис. 10.2).

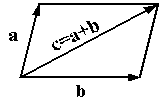
Сложение векторов называется сложением по правилу параллелограмма.

Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и .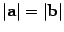

Вектор, противоположный вектору a, обозначается 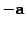, то есть .

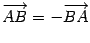Разностью векторов a и b называется сумма 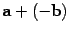. Разность обозначается 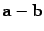, то есть .

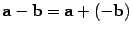Произведением вектора a на вещественное число 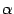называется вектор b, определяемый условием

1)
и, если 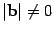, то еще двумя условиями:

2) вектор b коллинеарен вектору a;

3) векторы b и a направлены одинаково, если 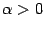, и противоположно, если .

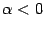Произведение вектора a на число 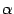обозначается 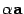(рис 1.4).

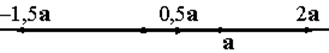
Рис.10.4.Умножение вектора на число

Когда речь идет о связи векторов с числами, то иногда числа называют скалярами. Таким образом, определение 10.9 задает умножение вектора на скаляр.

Рассмотрим некоторые свойства операций сложения и умножения вектора на число. Часть из них, которые будут особенно важны при обобщении понятия вектора, выделим в отдельную теорему.

Для любых векторов 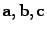и любых вещественных чисел 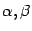выполняются следующие свойства:
1) 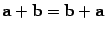(свойство коммутативности операции сложения);
2) 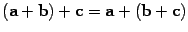(свойство ассоциативности операции сложения);
3) ;
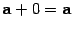4) ;
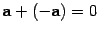5) 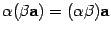(свойство ассоциативности по отношению к числам);
6) 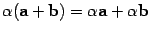(свойство дистрибутивности по отношению к умножению на число);
7) 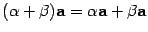(свойство дистрибутивности по отношению к умножению на вектор;
8) .

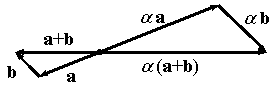
Случаи, когда 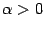или a и b коллинеарны, предоставляем проанализировать читателю самостоятельно.

Для доказательства свойства 7 заметим, что векторы 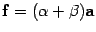и 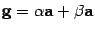коллинеарны. Без ограничения общности можно считать, что 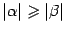(в противном случае поменяем местам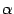и и 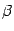в доказываемом равенстве).

Пусть 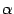и 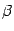одного знака. Тогда , .

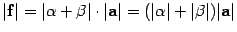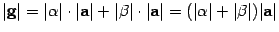Пусть 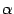и 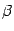имеют разные знаки. Тогда 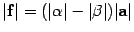, 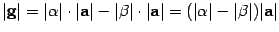. Получили, что 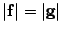в обоих случаях.

Векторы f и g имеют одно направление. Оно совпадает с направлением a при 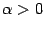и противоположно при 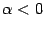. Следовательно, 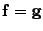. Свойство 7 доказано.

Свойство 8 очевидным образом вытекает из произведения вектора на число.

Из свойства ассоциативности следует, что в сумме векторов, содержащей три и более слагаемых, можно скобки не ставить. Как найти сумму нескольких слагаемых, не используя попарных сумм, видно из рисунка 10.7.

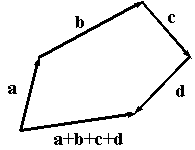
Сформулируем еще несколько очевидных свойств операций сложения и умножения вектора на число:
9) равенство 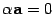верно тогда и только тогда, когда или , или ;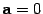
10) вектор, противоположный вектору a, равен 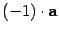, то есть ;
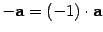11) для любых векторов a и b существует такой вектор x, что .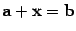

Date: 2015-09-05; view: 543; Нарушение авторских прав