
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача об оптимальном распределении ресурсов при выпуске продукции на предприятии (об ассортименте)
|
|
Методические указания к выполнению задач
Содержание
1. МОДЕЛИ ЗАДАЧ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
1.1. Задача об оптимальном распределении ресурсов при выпуске продукции на предприятии (об ассортименте)
1.2. Задача о смесях (рационе, диете)
1.3. Транспортная задача
1. 4. Модель рационального использования посевных площадей
1. 5. Модель рационального использования имеющихся мощностей
1.6. Задача о закреплении самолетов за воздушными линиями
1.7. Задача о ранце
1.8. Задача о назначениях
1.9. Задача коммивояжера
1.10. Задача о доставке (покрытии множества)
2. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПОМОЩЬЮ EXCEL
2.1. Ввод условий задачи
2.2. Работа в диалоговом окне "Поиск решения"
3. ПРИМЕРЫ РЕШЕНИЯ ОПТИМИЗАЦИОННЫХ ЗАДАЧ СРЕДСТВАМИ EXCEL
3.1. Получение требуемого сплава
3.2. Транспортная задача
3.3. Рациональное использование имеющихся площадей
3.4. Рациональное использование технологических участков
3.5. Закрепление самолетов за воздушными линиями
3.6. Задача о ранце
3.7. Назначение механизмов на работы
3.8. Задача коммивояжера
3.9. Задача о доставке
4. ВАРИАНТЫ ЗАДАНИЙ
Модели задач математического программирования
Задача об оптимальном распределении ресурсов при выпуске продукции на предприятии (об ассортименте)
Предположим, что предприятие выпускает n различных изделий. Для их производства требуются m различных видов ресурсов (сырья, вспомогательных материалов, рабочего и машинного времени и т.д.). Эти ресурсы ограничены и составляют в планируемый период b1, b2,..., bm условных единиц.
Известны также технологические коэффициенты aij, которые указывают, сколько единиц i-го ресурса требуется для производства изделия j-го вида (i=  j=
j= 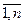 ).
).
Пусть прибыль, получаемая предприятием при реализации единицы изделия j-го вида, равна cj.
В планируемый период все показатели bi, aij и cj предполагаются постоянными.
Требуется составить такой план выпуска продукции, при реализации которого прибыль предприятия была бы наибольшей.
Сведем данные условия задачи в таблицу:
| Виды | Вид изделия | Запасы | |||||
| ресурсов | ... | j | ... | n | ресурсов | ||
| a11 | a12 | ... | a1j | ... | a1n | b1 | |
| a21 | a22 | ... | a2j | ... | a2n | b2 | |
| ... | ... | ... | ... | ... | ... | ... | ... |
| i | ai1 | ai2 | ... | aij | ... | ain | bi |
| ... | ... | ... | ... | ... | ... | ... | ... |
| m | am1 | am2 | ... | am2 | ... | amn | bm |
| Прибыль | c1 | c2 | ... | cj | cn |
Допустим, что предприятие будет выпускать xi изделий вида i. Требуется составить оптимальный план работы предприятия X={xj}, j= 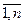 , т.е. найти такие значения переменных x1, x2,..., xn (объем выпуска продукции каждого вида), чтобы обеспечить предприятию получение максимальной прибыли от реализации всей продукции и чтобы на ее производство хватило имеющихся в распоряжении ресурсов.
, т.е. найти такие значения переменных x1, x2,..., xn (объем выпуска продукции каждого вида), чтобы обеспечить предприятию получение максимальной прибыли от реализации всей продукции и чтобы на ее производство хватило имеющихся в распоряжении ресурсов.
Математическая модель задачи выглядит следующим образом.
Целевая функция имеет вид:
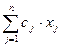 ® max.
® max.
Целевая функция (ЦФ) представляет суммарную прибыль.
Ограничения имеют вид:
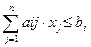 , i=
, i= 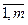 ,
,
Xj³ 0, j= 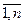 .
.
Уравнения ограничений модели представляют собой ограничения задачи по объему соответствующего ресурса, в ходе выполнения плана можно использовать либо весь запас этого ресурса либо часть его.
Date: 2015-09-19; view: 1088; Нарушение авторских прав