Задача о доставке (покрытии множества)

Фирма обслуживает некоторое количество клиентов (m). Каждый день она доставляет своим клиентам товары на грузовых машинах (или по железной дороге, воздушным путем, на баржах и т.д.). Существует множество допустимых маршрутов (n) доставки, каждый из которых позволяет обслужить определенное подмножество клиентов и требует использования в течении дня одного транспортного средства. Каждый маршрут характеризуется определенными расходами, которые могут соответствовать его длине, или стоимости расходуемого топлива и т.д. Цель состоит в том, чтобы выбрать такое множество маршрутов, при котором обеспечивается обслуживание каждого из клиентов, каждый клиент обслуживается один раз в день и суммарные расходы минимальны.

Введем переменные:

x_j=1, если маршрут j выбран;

x_j=0, в противном случае,

j= .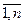

Обозначим элементы a_ij следующим образом:

a_ij=1, если i-й клиент обслуживается по маршруту j;

a_ij=0, в противном случае,

i= 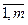, j= .

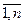Обозначим стоимость доставки по маршруту j через с_j.

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

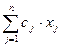® min.

ЦФ представляет суммарные расходы доставки по выбранным маршрутам.

Ограничения имеют вид:

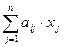=1, i= . (1)

Согласно условиям (1) каждый клиент обслуживается один раз в день.

Данная задача является задачей линейного булева программирования.

Date: 2015-09-19; view: 567; Нарушение авторских прав