
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Съемочное обоснование
|
|
Обычно съемочным обоснованием крупномасштабной съемки в условиях равнинной местности служат теодолитные ходы – полигонометрия низшего класса, а в пересеченной – сети микротриангуляции с короткими сторонами.
Теодолитным ходом называют замкнутый или разомкнутый многоугольник на местности, в котором измерены все стороны и углы. Для выполнения работ в заданной системе координат эти ходы привязывают к пунктам высшего класса.
Различают три вида теодолитных ходов: замкнутые, разомкнутые и висячие (Рисунок 65).
Для обеспечения крупномасштабных съемок пункты теодолитных ходов выбирают на участках с хорошим обзором. При съемке застроенной территории линии ходов должны проходить вдоль фасадной линии застройки.
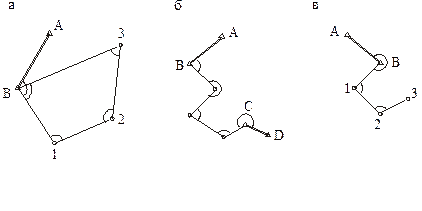 |
Рисунок 65 теодолитные ходы
Вершины ходов закрепляют на местности кольями или металлическими штырями. Средняя длина сторон хода может быть 100 – 200 м, минимальная – 20 м. Предельная длина ходов может быть до 600 м (для съемки масштаба 1:500) и 1500 м (в масштабе 1:1000). Длины линий в теодолитных ходах измеряются мерной рулеткой или точным дальномером с относительной погрешностью не хуже 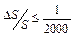 , а углы измеряются теодолитом одним полным приемом с точностью 0,5 – 1,0'.
, а углы измеряются теодолитом одним полным приемом с точностью 0,5 – 1,0'.
После выполнения полевых измерений приступают к их математической обработке, которая преследует три цели:
1) устранение геометрических несогласий в построенных фигурах;
2) оценку точности выполнения измерений;
3) вычисление координат пунктов теодолитного хода.
Исходными данными при прокладке теодолитного хода обычно служат как минимум два опорных пункта с известными координатами. В математическую обработку включаются все измеренные углы поворота и горизонтальные проекции длин линий. Дирекционные углы исходных сторон 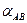 или
или 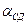 берут из каталога координат исходных пунктов или находят из решения обратных геодезических задач.
берут из каталога координат исходных пунктов или находят из решения обратных геодезических задач.
Математическую обработку начинают с определения геометрического несогласия в углах. В замкнутом ходе сумма внутренних углов должна быть равна 180º (n –2), а отличие суммы измеренных углов от этой величины составит угловую невязку
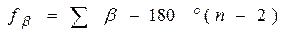 . (97)
. (97)
В разомкнутом ходе, проложенном между начальной и конечной сторонами с заданными дирекционными углами, угловые невязки получают по формулам:
 (98)
(98)
для левых по ходу углов поворота;
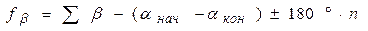 (99)
(99)
для правых углов поворота.
Невязки в углах не должны превышать величины
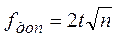 , (100)
, (100)
где t – точность измерения углов теодолитом.
Если невязка не выходит за пределы допуска, то ее распределяют между измеренными углами поровну, так что каждый угол получает поправку
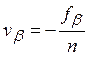 . (101)
. (101)
Сумма исправленных углов должна приводить к нулевой угловой невязке. После устранения угловой невязки последовательно вычисляют дирекционные углы всех сторон хода, используя исправленные углы поворота β:
 (102)
(102)
при левых углах поворота;
 (103)
(103)
для правых углов поворота.
При расчете по этим формулам следует иметь в виду, что дирекционные углы – положительные числа и находятся в пределах от 0˚ до 360˚.
Следующим этапом таких приближенных уравнительных вычислений будет вычисление приращений координат по всем сторонам хода
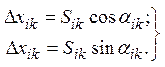 (104)
(104)
В замкнутом ходе суммы приращений координат теоретически должны быть равны нулю, и потому невязки в координатах
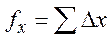 и
и 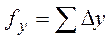 . (105)
. (105)
В разомкнутом ходе, проложенном между двумя опорными пунктами
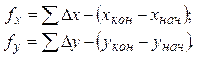
Полная линейная невязка определяется по теореме Пифагора
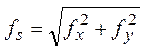 . (106)
. (106)
Ее считают допустимой при условии
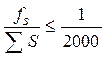 . (107)
. (107)
Если это условие выполнено, то невязки в координатах распределяют между приращениями координат с обратным знаком пропорционально длинам сторон хода, то есть каждое приращение получает поправку
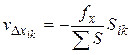 ;
; 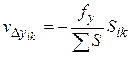 . (108)
. (108)
Если невязки составляют несколько сантиметров, то их можно распределить на глаз.
В заключение по исправленным приращениям координат последовательно вычисляют координаты всех точек хода, опираясь на исходные пункты.
Date: 2015-09-19; view: 967; Нарушение авторских прав