Понятие об управляемости системы и ее наблюдаемости

Рассмотрим случай, когда все переменные состояния могут быть измерены, а результаты этих действий могут быть использованы для управления системой. Однако такой случай не всегда технически реализуем. Поэтому для систем автоматического управления вводится понятие управляемости.

Рассмотрим линейную систему с постоянными коэффициентами:

,

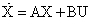(1)

где 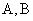– матрицы с постоянными коэффициентами.

При этом управление полагается скалярным, т.е. управление объектом осуществляется по одной координате.

Заданы начальная и конечная точка 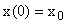, и 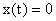. Задача состоит в том, чтобы перевести систему из заданного начального положения в некоторую точку, совпадающую с началом координат. При этом никаких ограничений на величину управляющего воздействия и время регулирования не накладывается. Если такая задача решается при любых начальных и конечных условиях, то такая система является управляемой.

Система называется управляемой, если существует такое управление, которое из любого начального состояния в любое конечное положение. При каких условиях система является управляемой. Попытаемся выяснить причины неуправляемости. Это удобно сделать с помощью геометрического представления движения системы. Как отмечалось выше решение линейного однородного уравнения имеет вид:

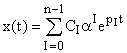
Если какой-нибудь из коэффициентов 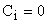, а остальные отличны от нуля, то движение происходит в инвариантном подпространстве матрицы 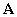. С геометрической точки зрения все траектории лежат в плоскости S, т.е. вектор 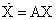также направлен вдоль этой плоскости. Предположим, что вектор 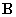тоже лежит в плоскости 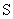. Очевидно, что добавка к вектору величины 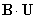оставляет вектор в той же плоскости, хотя и деформирует траекторию движения вектора состояния. Следовательно, если начальная точка лежит в плоскости 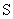, а конечная — нет, то попасть в точку с заданными координатами нельзя, так как не существует управления, которое переводит состояние системы с заданными параметрами из начальной точки в конечную. Такая система неуправляема по определению.

Условия управляемости в терминах исходной системы получены Калманом и имеют вид:

Для управляемости системы (1) необходимо и достаточно, чтобы выполнялось условие вида

.

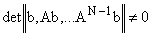(2)

Это условие выполняется, если матрица U вида

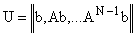
имеет ранг, равный N.

Рангом матрицы называется наибольший порядок ее определителя, отличный от нуля.

Рассмотрим поведение системы в пространстве состояний собственных векторов матрицы А (для простоты будем полагать, что собственные значения матрицы А — действительные и различные). Как мы убедимся в дальнейшем, в этом пространстве условия управляемости становятся практически очевидными. Введем неособое преобразование вида

,

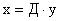(3)

где .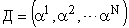

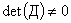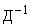Выше отмечалось, что и существует. Поэтому вектора X и Y связаны однозначной зависимостью. Следовательно, задачи об управляемости в пространствах этих переменных эквивалентны.

В пространстве новых переменных поведение САУ описывается уравнением

.

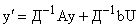(4)

Рассмотрим произведение

.

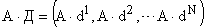так как 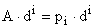, то

,

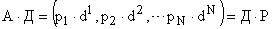где

Следовательно, уравнение (4) приводится к виду

.

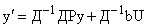или

.

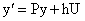(5)

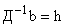— вектор столбец с компонентами .

Так как матрица Р диагональная, то

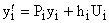, где .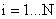

и если хотя бы одно 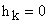, то координата — неуправляема. Поэтому можно предположить, что, если все 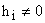, то система управляема.

Рассмотрим n-мерное пространство состояния Х, в котором каждому состоянию системы соответствует некоторое положение изображающей точки, определяемое значениями фазовых координат .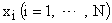

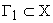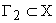Пусть в пространстве состояния заданы два множества и . Рассматриваемая система будет управляемой, если существует такое управление , определенное на конечном интервале времени , которое переводит изображающую точку в пространстве Х из подобласти 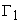в подобласть .

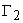Можно сузить определение управляемости и понимать под ней возможность перевода изображающей точки из любой области пространства состояний Х в начало координат. Система будет управляемой, если каждое состояние управляемо в этом смысле.

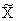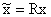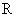От пространства состояний Х перейдем к другому пространству посредством неособого преобразования , причем , где — матрица коэффициентов .

Тогда вместо уравнения вида

,

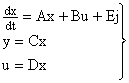(6)

где j — матрица возмущающих и задающих воздействий,

u — матрица-столбец управляющий величин,

y — матрица-столбец регулируемых величин,

x- матрица-столбец фазовых координат,

будем иметь

.

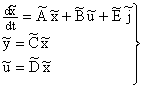(7)

Здесь использованы преобразованные матрицы коэффициентов:

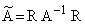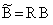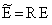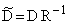, , , и .

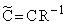Введение новых фазовых координат посредством неособого преобразования 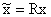приводит к эквивалентным системам различной структуры. При некотором преобразовании может оказаться, что часть управляющих величин не входит в некоторые дифференциальные уравнения (7) или часть фазовых координат не участвует в формирование вектора выходного сигнала 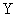. В первом случае система не будет полностью управляемой, а во втором — полностью наблюдаемой.

В случае не полностью управляемой системы ее исходное уравнение могут быть представлены в виде

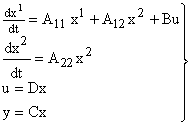
Это иллюстрирует рис. 7. Набор фазовых координат 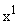соответствует управляемой части фазовых координат, а набор 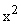— неуправляемой части.

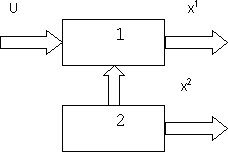
Рис. 7. Пример не полностью управляемой системы

Калманом был доказан критерий управляемости, который гласит, что размерность 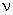управляющей части системы, то есть порядок первой группы уравнений (7) совпадает с рангом матрицы

,

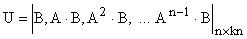где k — размерность управляющего вектора.

При система полностью управляема, при 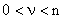— система не полностью управляема, при 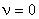— система полностью не управляема.

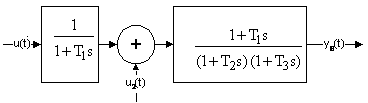
Рис. 8. Структура исходной системы.

На рис. 8 представлен простейший пример. Если рассматривать выходную величину 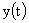при нулевых начальных условиях, то можно записать

,

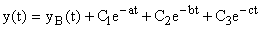где 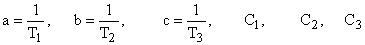определяются начальными условиям до приложения входного сигнал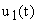а , а — вынужденная составляющая. Система устойчива при .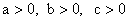

Если начальные условия до приложения управляющего сигнала были нулевыми, то поведение системы может быть рассчитано по передаточной функции

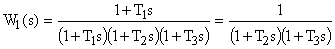
В этом случае переходный процесс в системе определяется как

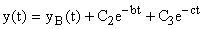
Как следует из последнего выражения, во втором случае система описывается дифференциальным уравнением не третьего, а второго порядка. Система будет устойчивой даже при .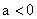

Рассмотренная система будет не полностью управляемой. В ней оказывается 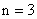, а .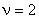

При введении второй составляющей управления 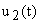система оказывается полностью управляемой, и ей будет соответствовать матрица-строка передаточный функций по управлению

.

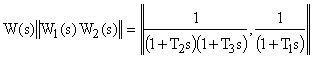В случае не полностью наблюдаемой системы ее уравнения могут быть представлены в виде

.

Эти уравнения отличаются от (7) тем, что фазовые координаты группы 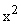не входят ни в выражения для 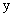и 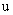, ни в первое уравнение, куда входят фазовые координаты группы 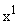. Группа фазовых координат 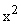относится к ненаблюдаемым.

Калманом показано, что порядок первой группы уравнений 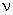совпадает с рангом матрицы V вида

.

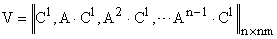При система полностью наблюдаема, при 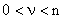— система не полностью наблюдаема, при 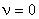— система полностью ненаблюдаемая.

На рис. 9 изображен простейший пример. Для него легко показать, что в формировании выхода участвуют только две фазовые координаты из трех.

Рис. 9. Пример не полностью наблюдаемой системы

В общем случае система может содержать четыре группы фазовых координат:

· управляемую, но ненаблюдаемую часть ,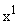

· управляемую и наблюдаемую часть ,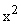

· неуправляемую и ненаблюдаемую часть ,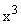

· неуправляемую но наблюдаемую част .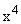

Исходные уравнения системы (7) можно для самого общего случая записать следующим образом:

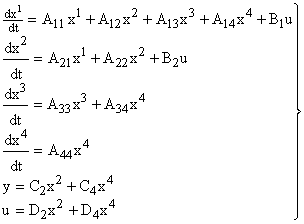
Левая часть характеристического уравнения

,

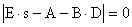где Е — единичная матрица размера , системы в этом случае содержит четыре сомножителя:

Управляемость и наблюдаемость системы в изложенном смысле не всегда совпадает с практическими представлениями. Даже если какая-либо фазовая координата и может быть вычислена по доступным для измерения выходным величинам обработка измеренных величин может быть, во-первых, сложной и, во-вторых, она может быть затруднена наличием помех. Поэтому практически наблюдаемыми координатами обычно считаются те из них, которые могут быть измерены датчиками различных типов.

Date: 2015-09-19; view: 831; Нарушение авторских прав