Механические системы

Механизмы передачи крутящих моментов широко используются для согласования скоростей рабочих машин или исполнительных механизмов и приводных двигателей. Среди них наибольшее распространение находят зубчатые передачи.

Рис. 5. Пример простейшей кинематической передачи.

Динамические процессы, происходящие в большинстве механизмов, неразрывно связаны со свойствами входящих в него механических систем. Особенности получения динамических моделей механизмов с линейными функциями положения и линейными характеристиками упругих звеньев можно рассмотреть на примере механической системы, представленной на рис. 5. Здесь ротор двигателя М и вращающееся исполнительное звено MM связаны передаточным механизмом, состоящим из зубчатых колес 1-4, образующих двухступенчатый редуктор. Пусть передаточное отношение первой пары — 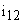, а 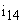– общее передаточное число редуктора. Моменты инерции всех звеньев относительно их собственных осей – .

При составлении динамической модели механизма будем учитывать крутильные податливости соединительных валов и зубчатых передач. При этом под податливостью понимается величина, обратная жесткости вала с, которая определяется как

,

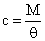где 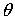— угол закручивания элемента механизма.

Вычисление податливости валов, связывающих элементы рассматриваемого механизма, подробно описано в литературе по теоретической и прикладной механике. Для вычисления жесткости зубчатой передачи со стальными зубьями можно пользоваться эмпирической зависимостью:

,

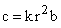где 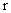– радиус ведущего колеса, см; 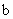– ширина зубчатого венца, см; .

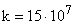Обозначим жесткости зубчатых передач 1-2 и 3-4 как 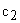и 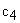соответственно. Жесткости валов, связывающих элементы механизма, обозначим как 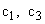и 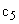. В большинстве своем упругие элементы передаточного механизма обладают диссипативными свойствами, то есть способностью рассеивать механическую энергию. В общем случае зависимость силы сопротивления от скорости может быть достаточно сложной функцией. Коэффициент, характеризующий диссипативные свойства, может быть непостоянным, а показатель степени, в которую возводится величина скорости, отличен от единицы. Решение таких задач выходит за рамки настоящего пособия. Будем рассматривать механические системы, в которых присутствуют силы вязкого трения, пропорциональные скорости движения элементов механизма. Эти силы характеризуются коэффициентами демпфирования . Иными словами, полагаем, что при изменении деформации 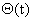элемента механизма с номером r возникает момент, определяемый как

.

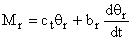Рассматриваемая система имеет шесть степеней свободы. В качестве обобщенных координат удобно принять углы поворота ротора двигателя и зубчатых колес, приведенные к ротору двигателя. То есть

, , ,

, , .

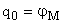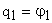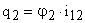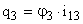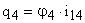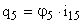При этом деформации валов и зубчатых колес, приведенные к валу двигателя, определяются как

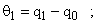
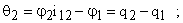
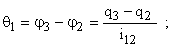
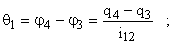
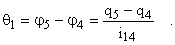
Из уравнения Лагранжа следует, что система дифференциальных уравнений, описывающая движение отдельных элементов механизма, может быть представлена в следующем виде

(7)

где 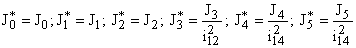– моменты инерции звеньев, приведенные к валу двигателя,

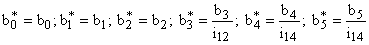— значения коэффициентов демпфирования, приведенные к валу двигателя,

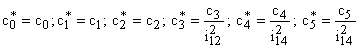— значения жесткости элементов кинематической цепи, приведенные к валу двигателя, 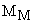– момент, развиваемый приводным двигателем,

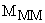– момент сопротивления рабочей машины.

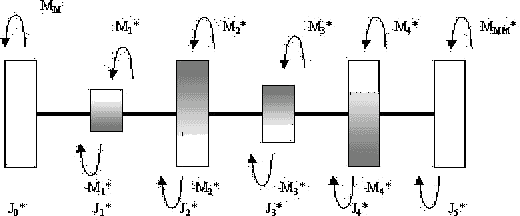
Рис. 6. Цепная динамическая модель механизма.

На рис. 6 представлена цепная динамическая модель механизма, для которой уравнения вынужденных колебаний, вызываемых активными приложенными силами и моментами инерции, совпадают с движениями, возникающими в системе, представленной выражением (7).

На рисунке 6 принято, что величина динамического момента 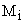определяется как

.

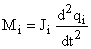Таким образом, динамические ошибки, вызванные податливостью звеньев, могут рассматриваться как вынужденные крутильные колебания многомассовой системы вблизи траектории программного движения механизма с абсолютно жесткими звеньями.

Система уравнений (7) в операторной форме записывается как

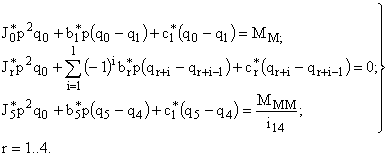
(8)

Из системы (8) определяются передаточные функции, связывающие законы изменения обобщенных координат с законами изменения обобщенных сил. Соответствующие им частотные характеристики имеют размерность податливости. Кроме того, возможно получение передаточных функций, связывающих величины обобщенных сил с моментами, прикладываемыми к редуктору со стороны двигателя и исполнительного механизма. Такие характеристики позволяют определить величины динамических моментов, возникающих в различных элементах механизма при разных режимах его работы.

Так как основные параметры зубчатых передач определяются исходя из требуемой нагрузочной способности, то в подавляющем большинстве случаев податливости спроектированных зубчатых колес значительно меньше податливостей элементов их соединения с рабочей машиной и приводным двигателем. Поэтому с достаточной степенью точности можно утверждать, что жесткости зубчатых колес общепромышленных механизмов бесконечно велики. Исходя из этого эвристического положения, двухступенчатый редуктор можно рассматривать как трехмассовую систему, параметры которой определяются следующим образом:

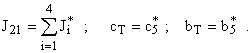
Структурная схема такого представления двухступенчатого редуктора показана на рис. 7.

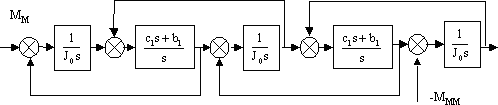
Рис. 7. Структурная схема механизма с двухступенчатым редуктором

На рис.8 изображены логарифмическая (а) и амплитудно-фазовая (б) частотные характеристики такого механизма.

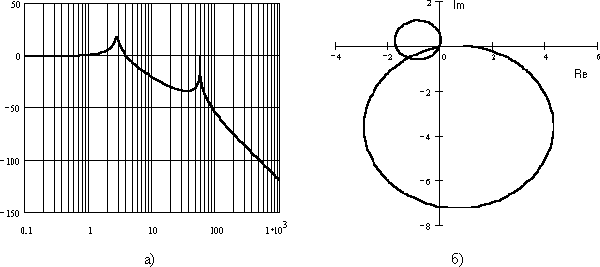
Рис. 8. Частотные характеристики двухступенчатого редуктора (а – логарифмическая, б — амплитудно-фазовая)

Date: 2015-09-19; view: 522; Нарушение авторских прав