Алгоритмы программ цифровых фильтров

Существует три основных алгоритма программной реализации дискретных передаточных функций (z -ПФ):

Алгоритм	Требуемое быстродействие	Объём памяти
Непосредственный а) с двумя буферами б) с одним буфером	24(m+k+1) / T ц	9m+9k+12
Последовательный	52k / T ц	20k+10
Параллельный	50k / T ц	19k+8

Дискретную ПФ можно представить в любой из форм:

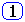
	W (z) =		Y (z)	=	b 0 +b 1 z -1 +...+b m z -m	- стандартная форма для дискретных ПФ
X (z)	a 0 +a 1 z -1 +...+a k z -k

	W (z) =		Y (z)	=	K		1 +e 2 z -1	...	1 +e k z -1	- разложение z -ПФ на множители [1]
X (z)	1 +d 1 z -1	1 +d 2 z -1	1 +d k z -1

	W (z) =		Y (z)	=	P 1	+	P 2	+...+	P k	- разложение z -ПФ на элементарные дроби [1]
X (z)	1 +d 1 z -1	1 +d 2 z -1	1 +d k z -1

где: e _i - нули z -ПФ; d _i - полюса z -ПФ; a ₀ - не равно нулю; P _i - коэффициенты разложения

Этим формам представления z -ПФ соответствуют структурные схемы изображенные на рис. 1.

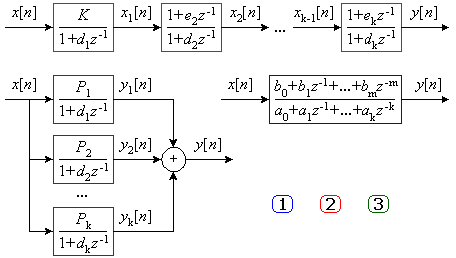
Рис. 1

• Разложения и 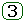делают параметры z -ПФ независимыми, позволяют контролировать ряд дополнительных фазовых координат: x ₁[ n ], x ₂[ n ],..., x _k-1[ n ]; или y ₁[ n ], y ₂[ n ],..., y _k[ n ] - что удобно при отладке систем.
• Последовательная структура 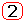удобна при синтезе дискретной коррекции.
• Параллельная структура 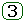удобна для построения цифровых регуляторов.
• Разложение z -ПФ на элементарные дроби 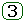позволяет реализовать z -ПФ на параллельно работающих ЦВМ для повышения быстродействия.

Перечисленные факторы определяют выбор алгоритма программы для ЦВМ.

После разложений, каждый из множителей в форме или каждую из элементарных дробей в форме следует представить в стандартной форме (с отрицательными степенями оператора z). Переход к разностным уравнениям будет един. z -ПФ в форме соответствует разностное уравнение (РУ):

,

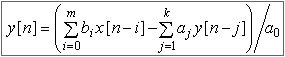по которому и составляется программа. Поскольку текущее значение выходной координаты y [ n ] рассчитывается по предыдущим значениям y [ n -1], y [ n -2], y [ n- k] - данное РУ называется рекурсивным.

Изобразим структурную схему цифрового фильтра для этого уравнения (см. рис. 2). Ее можно преобразовать, объединив два буфера (см. рис. 3). Цепочки элементов z ^-1 в программах будут соответствовать буферам из ячеек памяти, данные в которых сдвигаются на каждом такте дискретизации. Обе структурные схемы можно составить из простейших блоков программы VisSim.

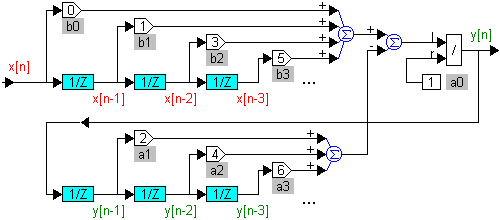
Структурной схеме соответствует алгоритм а.

Условие физической реализуемости - а ₀ ¹0

Рис. 2

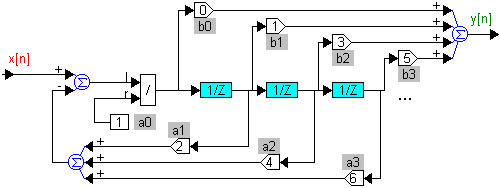
Структурной схеме соответствует алгоритм б.

Условие физической реализуемости - а ₀ ¹0

Рис. 3

Если выбран последовательный или параллельный алгоритм, то структура каждого множителя или элементарной дроби первого порядка (см. рис. 1) будет иметь более простой вид (см. рис. 4).

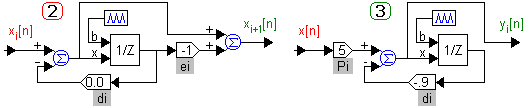
Рис. 4

Согласно структурной схеме рис. 2, составим процедуру реализующую дискретную ПФ второго порядка:

где: xz_2, xz_1 и yz_2, yz_1 - ячейки двух буферов, т.е. регистры задержки - z ^-1.

Date: 2015-09-19; view: 698; Нарушение авторских прав