Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Сумма А
|
|
|
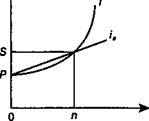
| Срок |
Рис. 4.1
Решение приведенного выше равенства дает следующие соотношения эквивалентности:
_ (1 + 0я
1,
(4.6)
/ - \1 + л/ - 1-
(4.7)
Аналогичным образом определим и другие, приведенные ниже, соотношения эквивалентности ставок.
Эквивалентность простых процентных ставок. При выводе искомых соотношений между ставкой процента и учетной ставкой следует иметь в виду, что при применении этих ставок используется временная база К= 360 или К= 365 дней. Если временные базы одинаковы, то из равенства соответствующих множителей наращения следует:
'* \-nd:
(4.8)
d' 1+w/
(4.9)
где п — срок в годах, /s — ставка простых процентов, ds — простая учетная ставка.
ПРИМЕР 4.3. Вексель учтен за год до даты его погашения по учетной ставке 15%. Какова доходность учетной операции в виде процентной ставки? По (4.8) находим
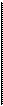0,15
's 1-0,15
= 0,17647, или 17,647%.
Иначе говоря, операция учета по учетной ставке 15% за год дает тот же доход, что и наращение по ставке 17,647%.
Следует обратить внимание на то, что отношения эквивалентности между простыми ставками is и ds существенно зависят от срока операции. Например, для d = 10 % находим следующие размеры эквивалентных ставок:
п (в годах) 0,1 0,5 1 2 5 10
/,(%) 10,1 10,5 11,1 12,5 20 оо
Пусть срок ссуды измеряется в днях, тогда, подставив в (4.8) и (4.9) п = t/K (напомним, что / — срок наращения процентов в днях, К — временная база), получим варианты соотношений эквивалентности:
а) временные базы одинаковы и равны 360 дням:
'--1бо^' (4|0>
360/
". = 15П^ <4">
б) если при начислении процентов принята база К = 365, а
для учетной ставки К = 360, то
/- 3654 (4.2)
° 360 -td/ ^Л1)
360/
ПРИМЕР 4.4. Необходимо найти величину учетной ставки, эквивалентной годовой процентной ставке 40% (К = 365) при условии, что срок учета равен 255 дням. Находим по формуле (4.13)
360 х 0,4 ЛОЛЛО|Г ЛЛЛо«,п,
d = 365 + 255 х 0,4 = °'30835' ИШ 3°'835%-
Эквивалентность простых и сложных ставок. Рассмотрим соотношения эквивалентности простых ставок is и ds, с одной стороны, и сложных ставок / и у, с другой. Сложную учетную ставку здесь не будем принимать во внимание. Попарно приравняв друг к другу соответствующие множители наращения, получим набор искомых соотношений.
Эквивалентность is и /. Формулы были получены выше (см. (4.6) и (4.7)).
| (4.14) (4.15) |
| (4.16) (4.17) (4.18) (4.19) |
Эквивалентность i uj:
| 4--а | + j/m)mn- 1 п |
| j -m | H/l+ >»",-1). |
| Эквивалентность ds и /: | |
| 4- | 1 - (1 + 0я п |
| / - | "J\-nds-l. |
| Эквивалентность ds и j: | |
| „,=± | -(1 +j/m)mn п |
j.mrn^\-nds-l).
ПРИМЕР 4.5. Какой сложной годовой ставкой можно заменить в контракте простую ставку 18% (К = 365), не изменяя финансовых последствий? Срок операции 580 дней.
По формуле (4.7) находим эквивалентную сложную ставку:
/•.580/збф + |§2018_1_017153/ или 17,153%.
I ODD
Эквивалентность сложных ставок. Остановимся только на соотношениях эквивалентности для ставок /, j и d. Имеем
/=(1 +j/ т)т- 1, (4.20)
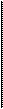y-mCVuT-l). (4.21)
Эквивалентность i и d:
«"TT7- <4И>
Приведем еще несколько полезных соотношений, которые нетрудно получить на основе приведенных выше формул с учетом того, что v = (1 + О""1:
d = /v, (4.24)
v = 1 - d, (4.25)
1 - d = Id. (4.26)
Заметим, что в зависимостях (4.22)—(4.26) срок не играет никакой роли.
ПРИМЕР 4.6. При разработке условий контракта стороны договорились о том, что доходность кредита должна составлять 24% годовых. Каков должен быть размер номинальной ставки при начислении процентов ежемесячно, поквартально?
У
12(12Vl24 - 1) - 0,21705; j - 4(Vl24 - 1) - 0,22100.
Date: 2015-09-19; view: 621; Нарушение авторских прав