Операции со сложной учетной ставкой

Учет по сложной учетной ставке. В практике учетных опера­ций иногда применяют сложную учетную ставку {compound dis- cound rate). В этих случаях процесс дисконтирования происхо­дит с замедлением, так как каждый раз учетная ставка приме­няется не к первоначальной сумме (как при простой учетной ставке), а к сумме, дисконтированной на предыдущем шаге во времени. Дисконтирование по сложной учетной ставке осуще­ствляется по формуле

Р =5(1 - d)\ (3.14)

где d — сложная годовая учетная ставка.

ПРИМЕР 3.11. Долговое обязательство на сумму 5 млн руб., срок оплаты которого наступает через 5 лет, продано с дискон­том по сложной учетной ставке 15% годовых. Каков размер полу­ченной за долг суммы и величина дисконта (в тыс. руб.)? Имеем

Р = 5000(1 - 0,15)⁵ = 2218,5; D = 5000 - 2218,5 = 2781,5.

Если применить простую учетную ставку того же размера, то

Р = 5000(1 - 5 х 0,15) = 1250; D = 5000 - 1250 = 3750.

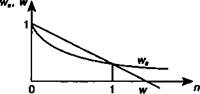
Как следует из приведенного примера, дисконтирование по сложной учетной ставке выгоднее для должника, чем по про­стой учетной ставке. Сказанное становится понятным при срав­нении формул для дисконтных множителей:

w_s = (1 - nd_s) Hw=(l-rf)«,

где d_s, d — простая и сложная учетные ставки соответственно.

Согласно первой из приведенных формул значение дисконт­ного множителя равномерно уменьшается по мере роста п и до-

стигает нуля при п = \/d. Согласно второй — множитель экс­поненциально уменьшается и достигает нуля лишь в пределе, при п = оо. Величины дисконтных множителей при применении простой и сложной учетных ставок показаны на рис. 3.S

Рис. 3.5

Номинальная и эффективная учетные ставки. Дисконтирова­ние может производиться не один, а т раз в году, т.е. каждый раз учет производится по ставке f/m. В этом случае

/>=£ 1

f\mn

т

(3.15)

где/— номинальная годовая учетная ставка.

Эффективная учетная ставка (d) характеризует степень дис­контирования за год. Определим ее на основе равенства дис­контных множителей:

откуда

f \mn (1-^ = |1-^|

d = 1

т

В свою очередь

/-m(l-*VT^f).

Эффективная учетная ставка во всех случаях, когда т > 1, меньше номинальной.

ПРИМЕР 3.12. По данным примера 3.11 определим сумму, полу­ченную при поквартальном учете по номинальной учетной ставке 15%, и эффективную учетную ставку. Имеем f = 0,15; т = 4; тп = 20;

P = 5000 1 - -^— = 2328,0 тыс. руб.

Date: 2015-09-19; view: 1571; Нарушение авторских прав