Конверсия валюты и наращение процентов

Рассмотренные выше методы наращения процентов позво­ляют перейти к обсуждению более сложных и важных в прак­тическом отношении задач. Остановимся на одной из них. Речь пойдет о совмещении операций конверсии (обмена) валюты и наращения процентов.

При возможности обмена рублевых средств на СКВ и обрат­ной конверсии целесообразно сравнить доходы от непосредст­венного размещения имеющихся денежных средств в депозиты и опосредованно через другую валюту. Сказанное относится и к получению дохода от СКВ при ее обмене на рубли, депони­ровании и обратной конверсии.

Возможны четыре варианта для наращения процентов с кон­версией денежных ресурсов и без нее:

без конверсии: СКВ -* СКВ;

с конверсией: СКВ — Руб — Руб — СКВ;

без конверсии: Руб -* Руб;

с конверсией: Руб — СКВ — СКВ — Руб.

Варианты с конверсией показаны на рис.2.7.

Р(СКВ)...... /...... S(CKB) Р(руб.)....... /...... S(py6.)

I, t *, t

Р(руб.)------ *-► S(py6.) P(CKB)---- '-+> S(CKB)

А б

Рис. 2.7

В операции наращения с конверсией валют существует два источника дохода — изменение курса и наращение процентов, причем, если второй из них безусловный (так как ставка про­цента фиксирована), то этого нельзя сказать о первом источни­ке. Более того, двойное конвертирование валюты (в начале и конце операции) может быть при неблагоприятных условиях убыточным. Решим в связи с этим две задачи. Определим сум­му в конце операции и ее доходность для двух вариантов опе­рации с конверсией.

Вариант СКВ -* Руб -* Руб -* СКВ. Проанализируем сначала вариант я, показанный на рис. 2.7. Примем обозначения:

P_v — сумма депозита в СКВ,

Р_г — сумма депозита в рублях,

S_v — наращенная сумма в СКВ,

S_r — наращенная сумма в рублях,

А^ — курс обмена в начале операции (курс СКВ в рублях),

К_{ — курс обмена в конце операции,

п — срок депозита,

/ — ставка наращения для рублевых сумм,

j — ставка наращения для конкретного вида СКВ.

Операция предполагает три шага: обмен валюты на рубли, наращение процентов на эту сумму и, наконец, конвертирова­ние в исходную валюту. Конечная (наращенная) сумма в валю­те определяется как

S_v = />Л (1 + ni) -jL. (2.20)

Три сомножителя этой формулы соответствуют трем пере­численным выше шагам. Множитель наращения т с учетом двойного конвертирования здесь имеет вид

_m = A_(1+m)=J_^. ₍2.21)

Взаимодействие двух факторов роста исходной суммы в этой формуле представлено наиболее наглядно. С ростом ставки множитель наращения линейно увеличивается, в свою очередь, рост конечного курса обмена уменьшает его.

ПРИМЕР 2.15. Предполагается поместить 1000 долл. на рубле­вом депозите. Курс продажи на начало срока депозита 26,08 руб. за $1, курс покупки доллара в конце операции 26,45 руб. Про­центные ставки: / = 22%; у = 15% (360/360). Срок депозита — 3 месяца.

З 22

— ■ —(1 + — х -==-* = 26,45 ^v 12 100

В свою очередь прямое наращение исходной долларовой сум­мы по долларовой ставке процента дает

S_v = 1000(1 + 0,25 х 0,15) = 1037,5 долл.

Продолжим анализ и поставим перед собой вторую задачу — измерим доходность операции в целом. В качестве измерителя доходности за срок операции примем простую годовую ставку процента /_э. Эта ставка характеризует рост суммы P_v до величи­ны 5_V:

S -Р

/ = у у

, т — 1

/^{Л =} —::—

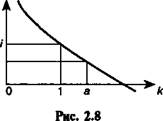
Данное выражение позволяет сделать ряд заключений, кото­рые удобно получить, обратившись к графику (см. рис. 2.8). Введем величину, характеризующую отношение последнего и первого курсов валюты:

* = А

v

С увеличением к эффективность операции падает. При к = 1 параметр /_э = /, при к > 1 параметр /_э < / (точка а на оси к), на­конец, при самой благоприятной для владельца денег ситуации (к < 1) имеем /_ > /.

Вариант Руб -* СКВ -* СКВ -* Руб. В этом варианте (см. рис. 2.7, б) трем шагам операции соответствуют три сомножителя формулы

5_Г= A(i + _nj)K_x = Р_г{\ + _Лу)А

(2.22)

Как и в предыдущем варианте, множитель наращения ли­нейно зависит от ставки, но теперь ставки процента для СКВ. Очевидно, что зависимости этого множителя от конечного кур­са или его темпа роста также линейные.

ПРИМЕР 2.16. Допустим, необходимо поместить на валютном депозите сумму в рублях (1 млн). Остальные условия — из приме­ра 2.15. Наращенная сумма в рублях к концу срока составит:

26 45 S, = 1000 х (1 + 0,25 х 0,15)-^^- = 1052,2 тыс. руб.

Оо

Прямое инвестирование в рублевый депозит дает больше: S_r = 1000 х (1 + 0,25 х 0,22) = 1055 тыс. руб.

Перейдем теперь к анализу эффективности операции. До­ходность операции определяется как

откуда

S - Р '^э~ Р_гп '

 

-(*<•

+ nj) - 1 \/п = (*(1 + nj) - \)/n. (2.23)

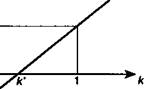
Зависимость показателя эффективности от к, как видим, ли­нейная. При к = 1 /_э =j (см. рис. 2.9), при £ > 1 /_э >у, нако­нец, при Л < 1 /_э <у, в частности, если к = к' = \/(\ + лу), опе­рация не принесет никакого дохода: /_э < 0.

'.А

У

Рис. 2.9

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Башарин Г. П. Начала финансовой математики. М.: ИНФРА-М, 1997.

2. Четыркин Е.М., Васильева Н. Е. Финансово-экономические расчеты. М.: Фи­нансы и статистика, 1990. Гл. 1.

3. Ковалев В.В., Уланов В.А. Курс финансовых вычислений. М.: Финансы и ста­тистика, 1994. Гл. 5.

4. Cartledge P. Financial arithmetic. A practitioners guide. Euromoney Books, 1993.

Глава 3 СЛОЖНЫЕ ПРОЦЕНТЫ

Date: 2015-09-19; view: 1051; Нарушение авторских прав