МЕХАНИКА Кинематика

Средняя скорость точки определяется отношением пути, пройденного точкой, ко времени, в течение которого этот путь прой­ден:

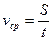
Физическая величина, характеризующая изменение скорости за единицу времени, на­зывается средним ускорением:

,

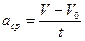где V и V₀ — конечная и начальная скорости движения.

В общем случае скорость прямолинейного движения

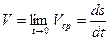а ускорение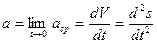

В случае прямолинейного равноперемен­ного движения скорость

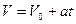
Путь, пройденный точкой при равнопере­менном движении,

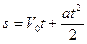
При криволинейном движении точки абсолютная величина полного ускорения

,

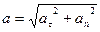где 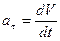тангенциальное (касательное) ускорение; 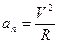нормальное (центростремительное) ускорение, где V₀ - скорость движения; R — радиус кривизны траектории.

Простейшим видом криволинейного движения является рав­номерное движение точки по окружности. При таком движении тангенциальное ускорение a_τ = 0, нормальное ускорение, называе­мое в этом случае центростремительным,

а_п = const.

Если точка движется по кругу радиуса R с линейной ско­ростью V, делая за время t n оборотов, то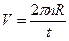

Кинематическими характеристиками вращательного движения тел служат угловое перемещение, угловая скорость и угловое ускорение. Угловым перемещением φ называется центральный угол, соответствующий дуге, пройденной движущейся точкой. Средняя угловая скорость ω_ср и среднее угловое ускорение ε_ср определяются аналогично средней скорости и среднему ускоре­нию прямолинейного движения, т. е.

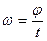и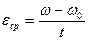

В общем случае угловая скорость криволинейного движения

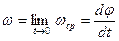
а угловое ускорение

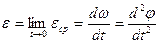
Для тел, движущихся с постоянным ускорением, аналогично прямолинейному движению, получаем:

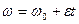
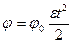
Параметры, характеризующие движение точки вращающегося тела, связаны с угловыми характеристиками соотношениями:

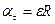
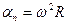
Изменение количества движения тела за определенный про­межуток времени равно импульсу действующей силы (второй закон Ньютона):

dk = Fdt,

где dk — изменение количества движения. Количество движения есть произведение массы тела т на скорость его движения v, т. е. k = mv; F — равнодействующая всех сил, приложенных к телу массой т; dt — промежуток времени, в течение которого на тело действовала сила.

Если масса тела постоянна, то второй закон динамики мож-но представить в виде

,

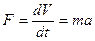где а — ускорение, приобретаемое телом массой т под действием силы F.

Тело массой m, движущееся поступательно со скоростью V, обладает кинетической энергией

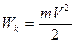
Потенциальная энергия тела, поднятого над поверхностью Земли (потенциальная энергия тела, находящегося на поверхности Земли, принимается равной нулю),

,

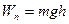где h — высота поднятия тела над поверхностью Земли;g - ускорение свободного падения.

Работу силы F при перемещении тела на пути s определяют по формуле

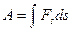
Работа постоянной силы выражается произведением силы, действующей в направлении перемещения, на величину этого перемещения s:

А = Fs cos a,

где а — угол между направлением действия силы и направле­нием перемещения.

Если тело массой т изменило свою скорость под действием силы от V₁ до V₂, то работа силы

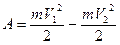
Мощность определяется по формуле

,

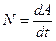а в случае постоянной мощности

,

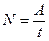где А — работа, совершаемая за время t.

Центростремительная сила, действующая на тело, движу­щееся по кривой,

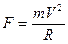
где R — радиус кривизны. В случае движения тела по окруж­ности он равен радиусу этой окружности.

Момент силы относительно оси вращения равен произведе­нию силы F на

плечо I:

,

где l— кратчайшее расстояние от оси вращения до линии дейст­вия силы.

Момент инерции / материальной точки равен произведению массы т материальной точки на квадрат расстояния г этой точки от оси вращения:

J=mr²

Момент инерции твердого тела

,

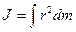где интегрирование должно проводиться по всему объему тела

Если для какого-либо тела известен его момент инерции /₀ от­носительно оси, проходящей через центр тяжести, то момент инерции / относительно любой оси, параллельной первой, может быть найден по формуле

J = J₀ + mа²,

где а — расстояние от центра тяжести тела до оси вращения; m — масса тела.

Момент инерции различных однородных тел массой m относи­тельно оси, проходящей через центр масс: шара радиусом R

,

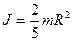цилиндра с внутренним радиусом r и внешним R (ось враще­
ния совпадает с геометрической осью цилиндра)

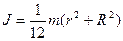
В частном случае момент инерции: тонкостенного цилиндра (R ≈ г)

J=mR²

сплошного цилиндра (г=0)

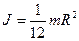
тонкого стержня длиной l (ось вращения проходит перпенди­кулярно стержню через его середину)

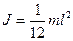
Изменение момента количества движения пропорционально величине приложенного момента силы и времени его действия (основное уравнение динамики вращательного движения):

dL = Mdt,

где dL — изменение момента количества движения. Момент ко­личества движения L равен произведению момента инерции / на угловую скорость вращения со, т. е. L = Jω₀; М — момент силы, приложенной к телу; dt — промежуток времени, в течение ко­торого на тело действовала сила. Момент импульса (момент количества движения) материальной точки

L_i=m_iv_ir_i

Момент импульса тела

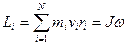
Если момент инерции тела постоянен, то основное уравне­ние динамики вращательного движения можно записать в виде

Jdω₀ = Mdt или М =Jε,

где ε — угловое ускорение.

Для изолированного тела, способного изменять момент инер­ции при вращении, закон сохранения момента количества дви­жения можно записать так:

L = const или Jω₀ = const.

Кинетическая энергия вращающегося тела

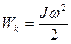
Кинетическая энергия тела, вращающегося с угловой ско­ростью ω вокруг оси, при поступательном движении оси со ско­ростью v

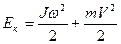
Элементарная работа во вращательном движении

dA=Mdφ

где М — момент силы, приложенной к телу. Работа силы при вращательном движении

где углы φ₁ и φ₂ соответствуют начальному и конечному положе­ниям радиуса-вектора любой точки твердого тела.

Сила, действующая на частицу со стороны окружающей жидко­сти, при центрифугировании

F₁ = ρ₀Vω²r,

где ρ₀ — плотность жидкости, V — объем частицы, ω — угловая скорость вращения, r — расстояние частицы от оси вращения.

Сила, действующая на частицу при ее движении по окружности,

F = ρ₁Vω²r,

где ρ₁ — плотность вещества частицы. При F₁≠F происходит перемещение частицы в направлении к оси вращения (при F₁> >F) или от оси (при F₁<.F).

Date: 2015-09-19; view: 370; Нарушение авторских прав