Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Производная. Применение производных для исследования функций
|
|
Предел
Функция y = f(x) имеет пределом число А при стремлении х к а, если для каждого числа е>0 найдется такое число δ>0, что
| y— A|<е, при | х —a|<δ
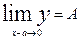
Основные теоремы о пределах Предел постоянной величины
limА=А.
Предел суммы (разности) конечного числа функций
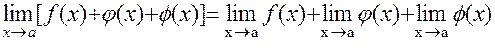
Предел произведений конечного числа функций
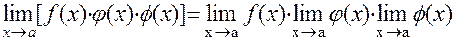
Предел частного двух функций:
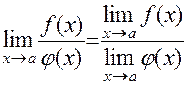при lim φ(x)≠0
Замечательные пределы:
, 
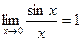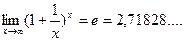
Производная. Применение производных для исследования функций
Производной функции f(x)называется предел отношения приращения функции Δу к приращению аргумента Δх в точке хпри стремлении Δх к нулю:
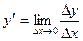
Производные некоторых функций:
| постоянной величины | у=С: | ý=0; |
| степенной функции | у = хμ: | ý=μxμ-1 |
| показательной функции в частности, если | у = аx: у = ех то | ý=axlna; ý= еx; |
| логарифмической функции натурального логарифма | y=logax у = lпх |  
|
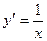
| тригонометрические функции: | y=sinx y=cos x y = tgx. y = ctgx. | y'=cosx;
ý =— sin x;
|
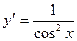
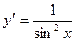
| обратных тригонометрические функции: | y=arcsinx y=arccosx y=arctgx y=arcctgx | 
|
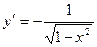
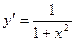
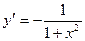
| Производная суммы (разности) функций | y = w±u: | y' = u'±v' |
| Производная произведения двух функций | y=uv | y' = u'v + v'u. |
| Производная частного двух функций | y=u/v: | 
|
| Производная сложной функции | y = f1(u), если y = f2(x), | у'x = у'ии'x |
Условие возрастания функции y = f(x)на отрезке [а, b]
f'(x)>0
Условие убывания функции y=f(x)на отрезке [а, b]
f'(x)<0
Условие максимума функции y=f(x)при x= а
f'(a)=0 и f'' (a)<0
Если при х=а производные f'(а) = 0 и f"(а) = 0, то необходимо исследовать f'(x)в окрестностях точки x = а. Функция у=f(х)при х=а имеет максимум, если при переходе через точку х= а производная f'(x)меняет знак с «+» на «-», в случае минимума — с «-» на «+» Если f'(x)не меняет знака при переходе через точку х = а,то в этой точке у функции экстремума нет
Date: 2015-09-19; view: 359; Нарушение авторских прав