Стандартные ряды частот вращения и подач

Привод считается регулируемым ступенчато, если при изменении частоты вращения может быть установлена не любая частота в пределах от n_min до n_max, а лишь ряд некоторых фиксированных значений. В подавляющем большинстве случаев ряды частот вращения или подач строят по законам геометрической прогрессии. Это означает, что частоты вращения в указанных пределах будут составлять ряд

n_1; n_2; n_{3; ……} n_i; n_{i+1; …….}n_z-1; n_z ,

причем величина 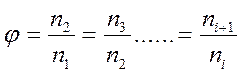называется знаменателем геометрического ряда.

Широкое применение геометрического ряда связано с тем, что конструкция коробок скоростей и подач, обеспечивающих такой ряд, получается наиболее простой (так называемое “конструктивное преимущество геометрического ряда”).

Кроме того, еще в 1876 году академик Гадолин показал, что возможная “потеря производительности” при использовании геометрического ряда есть величина постоянная и зависит только от величины знаменателя ряда .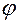

В самом деле, рассчитанное технологом по формулам оптимальное значение частоты вращения n практически никогда не совпадает со значениями применяемого на станке ряда и поэтому не может быть установлено точно. Величина n оказывается в промежутке между двумя какими-либо соседними значениями n_i и n_i+1. Очевидно, что, даже если значение n будет весьма близко к n_i+1, придется установить на станке ближайшее меньшее значение n_i, поскольку стойкость инструмента обратно пропорциональна скорости резания в пятой степени, и незначительное увеличение скорости резания против оптимальной приведет к катастрофическому уменьшению стойкости. Производительность прямо пропорциональна скорости, поэтому наибольшая возможная относительная потеря производительности в пределе будет равна:

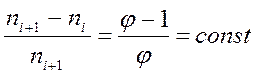
Таким образом, заказывая станок с коробкой скоростей, обеспечивающей геометрический ряд с тем или иным значением знаменателя 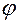, технолог заранее знает возможные значения относительной потери производительности.

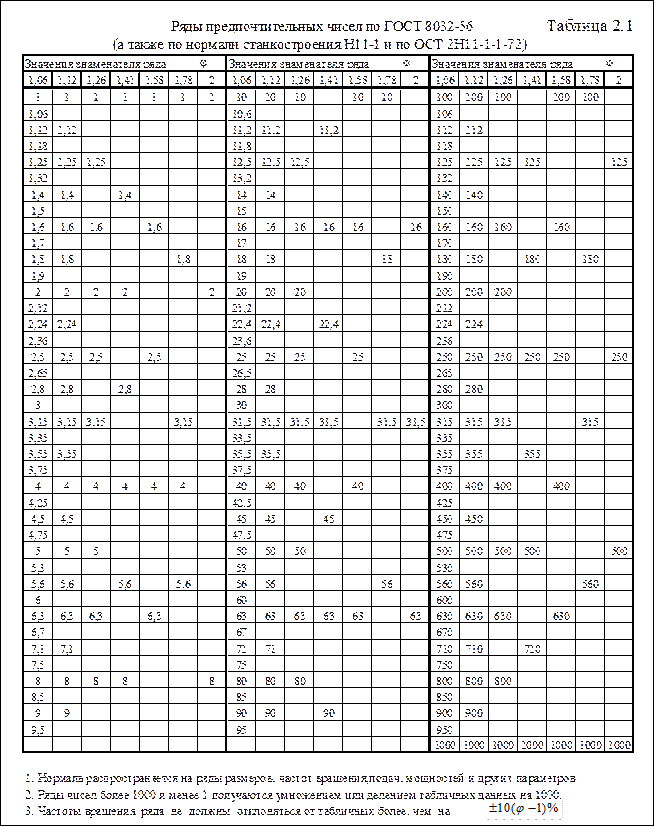
В станкостроении применяются геометрические ряды, регламентируемые стандартом ГОСТ 8032-56 “Ряды предпочтительных чисел”. Принятые в стандарте значения знаменателей ряда 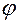и значения чисел в рядах от 1 до 1000, приведены в таблице 2.1.

В стандарте использовано семь геометрических рядов со следующими знаменателями:

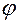= 1,06; 1,12: 1,26; 1,41; 1,58; 1,78; 2,0

Каждый стандартный знаменатель ряда является целой четной степенью наименьшего знаменателя 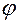= 1,06:

1,12=1,06²; 1,26=1,06⁴; 1,41=1,06⁶; 1,58=1,06⁸; 1,78=1,06¹⁰; 2=1,06¹²

Следовательно, ряд с любым знаменателем может быть образован из основного ряда (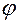 =1,06) путем отбрасывания отдельных его членов через один, три, пять и т.д., что хорошо видно в таблице 2.1.

В очень редких случаях в некоторых механизмах станков используют не геометрический ряд, а другой закономерный ряд, например – арифметический.

Так поступают при конструировании коробок подач токарно-винторезных станков для того, чтобы обеспечить нарезание стандартных резьб, у которых шаги также образуют арифметический ряд. Однако в подавляющем большинстве случаев, если проектируется ступенчато регулируемый привод, то ряд частот вращения или подач строится по законам геометрической прогрессии.