Поверхности второго порядка

Эллипсоид – это поверхность в пространстве R³, которая задается уравнением

(1)

Изучим строение поверхности методом сечений. Рассмотрим сечения плоскостями, параллельными координатным плоскостям.

1) Пусть x=x₀. Это плоскость, параллельная координатной плоскости Oyz. Тогда

или

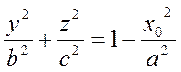(2)

Разделим обе части уравнения (2) на выражение, стоящее в правой части:

(3)

Очевидно, что это каноническое уравнение центрального эллипса с полуосями

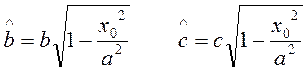(4)

Такой эллипс существует лишь в том случае, когда выполняется естественное ограничение на подкоренное выражение:

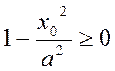
или

(5)

2) Пусть y=y₀. Это плоскость, параллельная координатной плоскости Oxz. Тогда

или

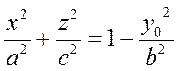(6)

Разделим обе части уравнения (6) на выражение, стоящее в правой части:

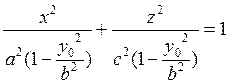(7)

Очевидно, что это каноническое уравнение центрального эллипса с полуосями

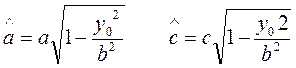(8)

Такой эллипс существует лишь в том случае, когда выполняется естественное ограничение на подкоренное выражение:

или

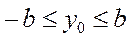(9)

3) Пусть z=z₀. Это плоскость, параллельная координатной плоскости Oxy. Тогда

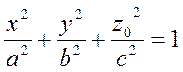
или

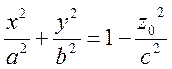(10)

Разделим обе части уравнения (6) на выражение, стоящее в правой части:

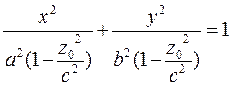(11)

Очевидно, что это каноническое уравнение центрального эллипса с полуосями

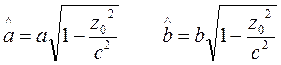(12)

Такой эллипс существует лишь в том случае, когда выполняется естественное ограничение на подкоренное выражение:

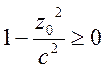
или

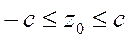(13)

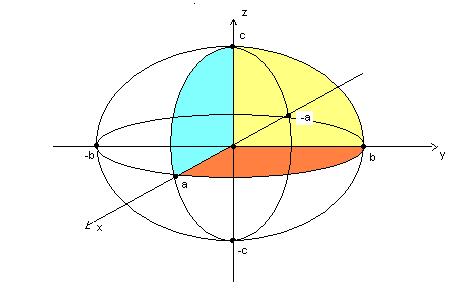
Рис.1

Однополостный гиперболоид – это поверхность в пространстве R³, которая задается уравнением

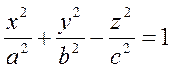(14)

Изучим строение этой поверхности методом сечений. Рассмотрим сечения плоскостями, параллельными координатным плоскостям.

1) Пусть x=x₀. Это плоскость, параллельная координатной плоскости Oyz. Тогда

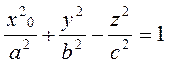
или

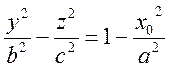(15)

Разделим обе части уравнения (2) на выражение, стоящее в правой части:

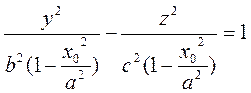(16)

Очевидно, что это каноническое уравнение центральной гиперболы с полуосями

(17)

и асимптотами

(18)

2) Пусть y=y₀. Это плоскость, параллельная координатной плоскости Oxz. Тогда

или

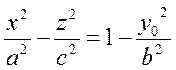(10)

Разделим обе части уравнения (10) на выражение, стоящее в правой части:

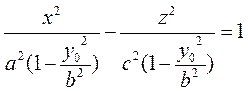(11)

Очевидно, что это каноническое уравнение центральной гиперболы с полуосями

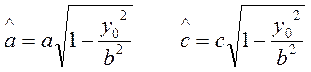(12)

Такая гипербола существует лишь в том случае, когда выполняется естественное ограничение на подкоренное выражение:

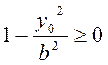
или

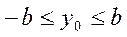(13)

3) Пусть z=z₀. Это плоскость, параллельная координатной плоскости Oxy. Тогда

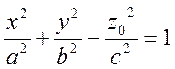
или

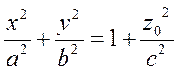(14)

Разделим обе части уравнения (14) на выражение, стоящее в правой части:

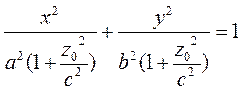(15)

Очевидно, что это каноническое уравнение центрального эллипса с полуосями

(16)

При z₀=0 получаем эллипс наименьшего размера, а именно

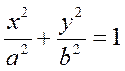(17)

Рис.2

Двухполостный гиперболоид – это поверхность в пространстве R³, которая задается уравнением

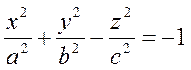(19)

Изучим строение этой поверхности методом сечений. Рассмотрим сечения плоскостями, параллельными координатным плоскостям.

1) Пусть x=x₀. Это плоскость, параллельная координатной плоскости Oyz. Тогда

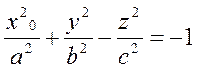
или

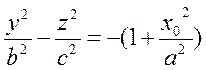(20)

Разделим обе части уравнения (20) на выражение, стоящее в правой части:

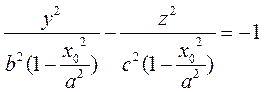(21)

Очевидно, что это каноническое уравнение сопряженной центральной гиперболы с полуосями

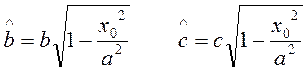(22)

и асимптотами

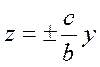(23)

2) Пусть y=y₀. Это плоскость, параллельная координатной плоскости Oxz. Тогда

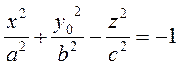
или

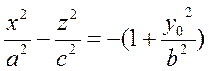(24)

Разделим обе части уравнения (24) на выражение, стоящее в правой части:

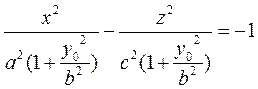(25)

Очевидно, что это каноническое уравнение сопряженной центральной гиперболы с полуосями

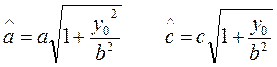(26)

и с асимптотами

(27)

3) Пусть z=z₀. Это плоскость, параллельная координатной плоскости Oxy. Тогда

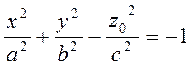
или

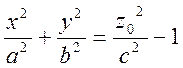(28)

Разделим обе части уравнения (28) на выражение, стоящее в правой части:

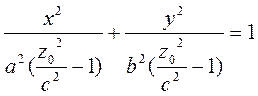(29)

Очевидно, что это каноническое уравнение центрального эллипса с полуосями

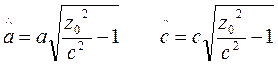(30)

Из (30) видно, что

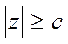
или

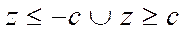
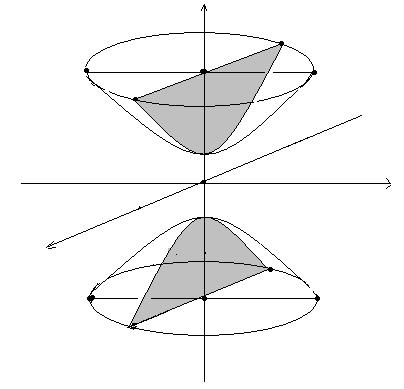
Рис. 3

Эллиптический параболоид – это поверхность в пространстве R³, которая задается уравнением

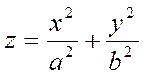(31)

Изучим строение этой поверхности методом сечений. Рассмотрим сечения плоскостями, параллельными координатным плоскостям.

1) Пусть x=x₀. Это плоскость, параллельная координатной плоскости Oyz. Тогда

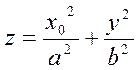
или

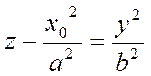(32)

Очевидно, что это каноническое уравнение параболы с вершиной в точке

и ветвями в направлении оси Oz.

2) Пусть y=y₀. Это плоскость, параллельная координатной плоскости Oxz. Тогда

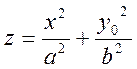
или

(33)

Очевидно, что это также каноническое уравнение параболы с вершиной в точке

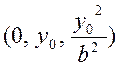
и ветвями в направлении оси Oz.

3) Пусть z=z₀. Это плоскость, параллельная координатной плоскости Oxy. Тогда

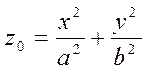(34)

Разделим обе части уравнения (34) на z₀:

Это каноническое уравнение центрального эллипса с полуосями .

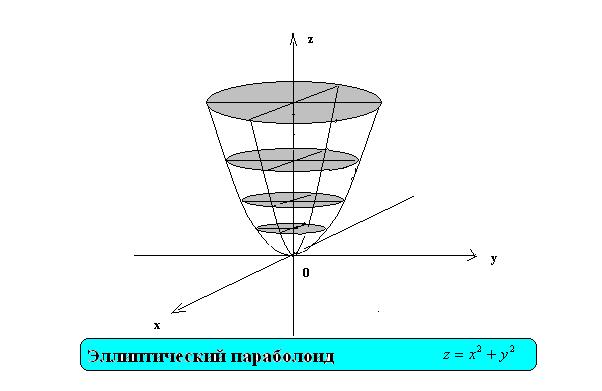
Рис. 4

Ниже представлен рисунок, выполненный в среде Mathcad и представляющий также эллиптический параболоид

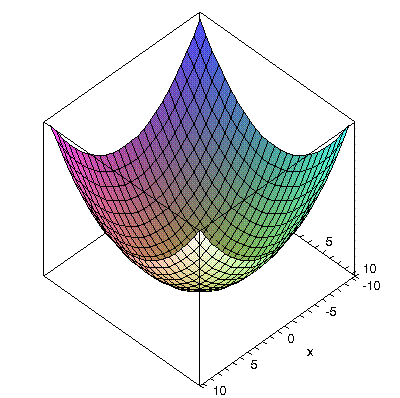
Рис. 5

Конус – это поверхность в пространстве R³, которая задается уравнением

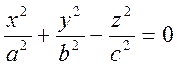(19)

Изучим строение этой поверхности методом сечений. Рассмотрим сечения плоскостями, параллельными координатным плоскостям.

1) Пусть x=x₀. Это плоскость, параллельная координатной плоскости Oyz. Тогда

или

(20)

Разделим обе части уравнения (20) на выражение, стоящее в правой части:

(21)

Очевидно, что это каноническое уравнение сопряженной центральной гиперболы с полуосями

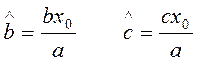(22)

и асимптотами

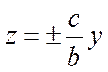(23)

2) Пусть y=y₀. Это плоскость, параллельная координатной плоскости Oxz. Тогда

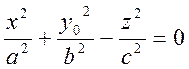
или

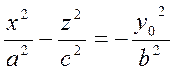(24)

Разделим обе части уравнения (24) на выражение, стоящее в правой части:

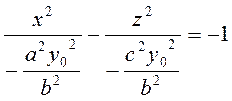(25)

Очевидно, что это каноническое уравнение сопряженной центральной гиперболы с полуосями

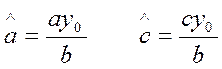(26)

и с асимптотами

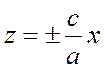(27)

3) Пусть z=z₀. Это плоскость, параллельная координатной плоскости Oxy. Тогда

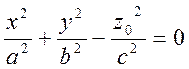
или

(28)

Разделим обе части уравнения (28) на выражение, стоящее в правой части:

(29)

Очевидно, что это каноническое уравнение центрального эллипса с полуосями

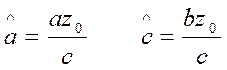(30)

Из (30) видно, что

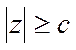
или

Рис. 6

Date: 2015-09-03; view: 479; Нарушение авторских прав