Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Эллипсоид
|
|
Исследуем поверхность, заданную уравнением
(28)
Рассмотрим сечения поверхности (28) с плоскостями, параллельными плоскости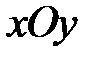 
. Уравнения таких плоскостей: 
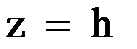, где 
любое число.
Линия, получаемая в сечении, определяется двумя уравнениями
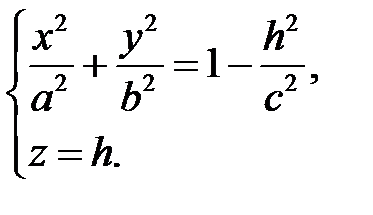(29)
Исследуем уравнения (29):
а) Если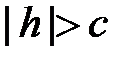 
, 
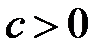, то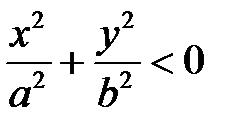 
. Точек пересечения поверхности (28) с плоскостями 
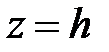не существует.
б) Если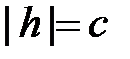 
, т. е. 
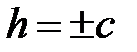, то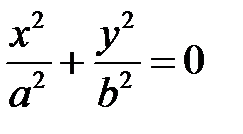 
. Линия пересечения (29) вырождается в две точк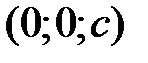и 
и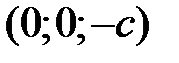 
. Плоскост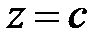и 
и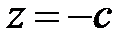 
касаются данной поверхности.
в) Если 
, то уравнения (29) можно переписать в виде:
Как видно, линия пересечения есть эллипс с полуосям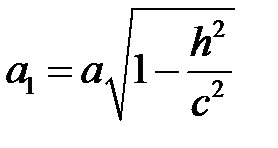и 
и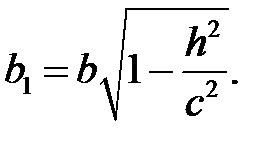 
При этом чем меньше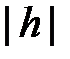 
, тем больше полуоси 
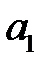и 
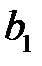. При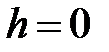 
они достигают своих наибольших значений: 
, 
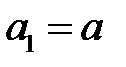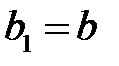. Уравнения (29) примут вид
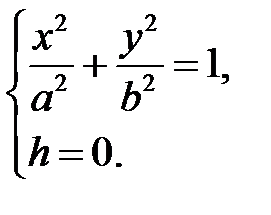
Аналогичные результаты получим, если рассмотрим сечения поверхности (28) плоскостям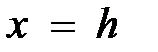и 
и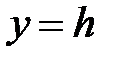 
.
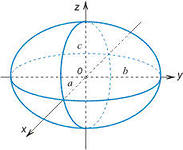
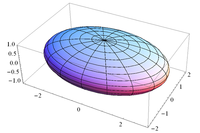
Таким образом, рассмотренные сечения позволяют изобразить поверхность (28) как замкнутую овальную поверхность. Поверхность (28) называется эллипсоидом. Величины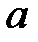 
, 
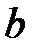и 
называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехосным; если какие-либо две полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения; если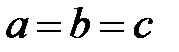 
, то 
в сферу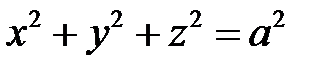 
.
Date: 2015-09-03; view: 350; Нарушение авторских прав