
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример решения задачи Д4
|
|
К невесомому валу АВ, закрепленному в точке А подпятником и в точке В – подшипником и вращающемуся с постоянной угловой скоростью w, жестко прикреплены невесомый стержень 1 длиной L1, имеющий на конце груз массой m1, и тело 2 в виде сплошной однородной квадратной пластины со стороной L2 и массой m2 (рис. Д4).
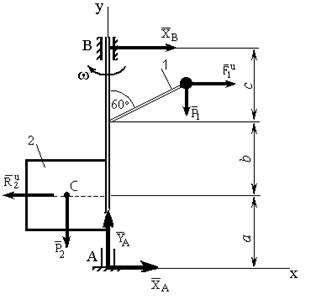
Рис. Д4
Д а н о: a = b = с = 0,5 м; L1 = 0,4 м; m1 = 2 кг; L2 = 0,6 м; m2 = 8 кг; w = 4 с-1.
О п р е д е л и т ь: реакции подпятника А и подшипника В.
 Р е ш е н и е
Р е ш е н и е
Для определения искомых реакций рассмотрим движение механической системы, состоящей из вала АВ, пластины и груза, и применим принцип Даламбера. Проведём вращающиеся вместе с валом оси xАy так, чтобы стержень и пластина лежали в плоскости xy, и покажем действующие на систему внешние силы: силы тяжести 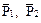 , составляющие реакции подпятника
, составляющие реакции подпятника 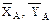 и реакцию подшипника
и реакцию подшипника 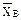 .
.
Согласно принципу Даламбера покажем на рисунке силу инерции груза 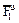 , считая груз материальной точкой, и главный вектор сил инерции пластины
, считая груз материальной точкой, и главный вектор сил инерции пластины 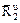 . Так как вал вращается равномерно (w = const), то элементы пластины имеют только нормальные ускорения, направленные к оси вращения. Тогда силы инерции будут направлены от оси вращения.
. Так как вал вращается равномерно (w = const), то элементы пластины имеют только нормальные ускорения, направленные к оси вращения. Тогда силы инерции будут направлены от оси вращения.
Величина главного вектора сил инерции пластины
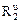 = m2× a C,
= m2× a C,
где a C – ускорение центра масс пластины, при этом a C = w2 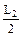 .
.
В результате
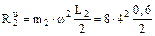 = 38,4 H.
= 38,4 H.
Аналогично для силы инерции  груза
груза
 = m1×w2×L1×sin 60° = 2×42×0,4
= m1×w2×L1×sin 60° = 2×42×0,4 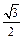 = 11,1 H.
= 11,1 H.
Так как все действующие силы и силы инерции лежат в плоскости ху, то и реакции подпятника А и подшипника В тоже лежат в этой плоскости, что было учтено при их изображении.
По принципу Даламбера действующие на тела системы внешние силы и приложенные силы инерции образуют уравновешенную систему сил. Составляя для этой плоской системы произвольно расположенных сил уравнения равновесия, получим
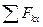 = 0;
= 0; 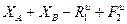 = 0, (1)
= 0, (1)
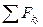 = 0; YA -P1-P2 =0, (2)
= 0; YA -P1-P2 =0, (2)
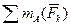 = 0;
= 0; 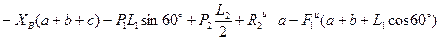 =0 (3)
=0 (3)
Подставив в эти уравнения числовые значения всех заданных по условию задачи и вычисленных величин и решив эту систему уравнений, найдём искомые реакции.
О т в е т: XA = 4,7 H; YA = 98,1 H;, XB = 22,6 H.
Задание Д5. Уравнение Лагранжа II рода
Механическая система (см. рис. Д3.0–Д3.9 к задаче Д3) состоит из ступенчатых шкивов 1 и 2 с радиусами ступеней R1 = R, r1 = 0,4R; R2 = R, r2 = 0,8R (массу каждого шкива считать равномерно распределенной по его внешнему ободу); грузов 3, 4 и сплошного однородного цилиндрического катка 5. Вес каждого тела соответственно указан в табл. Д5 (столбцы 2–6). Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Грузы скользят по плоскостям без трения, а катки катятся без скольжения. Кроме сил тяжести, на одно из тел системы действует постоянная сила 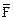 , а на шкивы 1 и 2 при их вращении – постоянные моменты сил сопротивления, равные, соответственно, М1 и М2, величины которых также приведены в табл. Д5 (столбцы 7–9).
, а на шкивы 1 и 2 при их вращении – постоянные моменты сил сопротивления, равные, соответственно, М1 и М2, величины которых также приведены в табл. Д5 (столбцы 7–9).
Требуется составить для данной системы уравнение Лагранжа и определить из него величину, указанную в столбце 10 табл. Д5, где e1, e2 – угловые ускорения шкивов 1 и 2, a 3, a 4, a C5 – ускорения грузов 3, 4 и центра масс катка 5 соответственно. Когда в задаче надо определить e1 или e2 , принимают R = 0,25 м. Тот из грузов 3, 4, вес которого равен нулю, на чертеже не изображать. Шкивы 1 и 2 всегда входят в систему.
Т а б л и ц а Д5
| Номер условия | Вес тела, Н | Момент сопротивления, Нм | Сила F, H | Найти | |||||
| Р1 | Р2 | Р3 | Р4 | Р5 | М1 | М2 | |||
| 2R | a 3 | ||||||||
| 3R | ε2 | ||||||||
| 3R | ε1 | ||||||||
| 2R | a 3 | ||||||||
| 3R | a C5 | ||||||||
| 4R | ε1 | ||||||||
| 2R | a 4 | ||||||||
| 3R | ε2 | ||||||||
| 2R | a 4 | ||||||||
| 2R | a C5 |
Указания. В задаче Д5 механическая система имеет одну степень свободы, следовательно, ее положение определяется одной обобщенной координатой и для нее должно быть составлено одно уравнение.
За обобщенную координату q принимают:
-перемещение х соответствующего груза или центра масс катка 5 (в задачах, где требуется определить a 3 , a 4 или a C5);
-угол поворота j соответствующего шкива (в задачах, где требуется определить e1 или e2).
Для составления уравнения необходимо вычислить сначала кинетическую энергию системы Т и выразить все вошедшие в Т скорости через обобщенную скорость, т.е. через 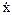 , если обобщенная координата х, или через
, если обобщенная координата х, или через 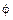 , если обобщенная координата j. Затем вычислить обобщенную силу Q. Для этого надо сообщить системе возможное перемещение, при котором выбранная координата, т.е. х (или j), получает положительное приращение dx (или dj), и вычислить сумму элементарных работ всех сил на этом перемещении; в полученном равенстве надо все другие элементарные перемещения выразить через δx (или δφ) и вынести δx (или δφ) за скобки. Коэффициент при δx (или δφ) и будет обобщенной силой Q.
, если обобщенная координата j. Затем вычислить обобщенную силу Q. Для этого надо сообщить системе возможное перемещение, при котором выбранная координата, т.е. х (или j), получает положительное приращение dx (или dj), и вычислить сумму элементарных работ всех сил на этом перемещении; в полученном равенстве надо все другие элементарные перемещения выразить через δx (или δφ) и вынести δx (или δφ) за скобки. Коэффициент при δx (или δφ) и будет обобщенной силой Q.
Date: 2015-09-03; view: 763; Нарушение авторских прав