Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Квадратичная форма
|
|
Функция F (x 1, x 2, …, xn)=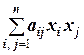 
называется квадратичной формой от переменных x 1, x 2, …, xn, если aij = aji для всех i, j Î{1, 2, …, n }. Матрицей квадратичной формы 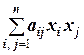называется матрица A =(aij) n ´ n. Таким образом, матрица квадратичной формы является симметрической.
Квадратичная форма 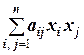и соответствующая ей матрица A =(aij) n ´ n называются положительно (отрицательно) определённой, если для любого ненулевого X =(x 1, x 2, …, xn) выполняется неравенство 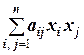>0 ( <0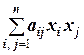). Тот факт, что 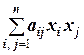является положительно (отрицательно) определённой, обозначается через A >0 (A <0).
Аналогично, квадратичная форма называется положительно (отрицательно) полуопределённой, если для любого X выполняется неравенство 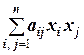³0 (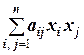 £0) и существует ненулевой вектор X, такой, что 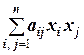=0. Обозначение: A ³0 (A £0).
Квадратичная форма называется знаконеопределённой, если существуют такие векторы X =(x 1, x 2, …, xn) и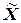 
=(
, 
, …, 
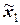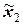), что выполняются неравенства 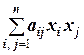>0 и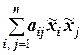 
<0. Обозначение: А 
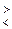0.
1.6.1. Для того, чтобы матрица была положительно определённой, необходимо и достаточно, чтобы все угловые миноры матрицы были положительными:
D1>0, D2>0, …, D n >0.
Для того, чтобы матрица была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров чередовались, начиная с отрицательного:
D1<0, D2>0, …, (-1) n D n >0.
Для того, чтобы матрица была положительно полуопределённой, необходимо и достаточно, чтобы все главные миноры матрицы были ненулевыми.
Для того, чтобы матрица была отрицательно полуопределённой, необходимо и достаточно, чтобы все главные миноры чётного порядка были неотрицательны, а все главные миноры нечётного порядка были неположительны.
Таким образом, если для квадратичной формы не выполняется ни одно из вышеперечисленных условий 1.6, то она является знаконеопределённой.
Ясно, что при достаточно больших п для проверки знакоопределённости квадратичной формы использование миноров (как угловых, так и главных) не очень удобно. Иногда удобно использование собственных векторов.
1.6.2. Для того, чтобы матрица была положительно определённой, необходимо и достаточно, чтобы все собственные значения были положительными:
l 1>0, l 2>0, …, ln >0.
Для того, чтобы матрица была отрицательно определённой, необходимо и достаточно, чтобы все собственные значения были отрицательными:
l 1<0, l 2<0, …, ln <0.
Для того, чтобы матрица была положительно полуопределённой, необходимо и достаточно, чтобы все собственные значения были неотрицательными:
l 1³0, l 2³0, …, ln ³0.
Для того, чтобы матрица была отрицательно полуопределённой, необходимо и достаточно, чтобы все собственные значения были неположительными:
l 1£0, l 2£0, …, ln £0.
Наконец, квадратичная форма является знаконеопределённой тогда и только тогда, когда собственные значения матрицы квадратичной формы принимают различные знаки.
Date: 2015-09-03; view: 650; Нарушение авторских прав