Приклад виконання завдання. До вантажу 1 (рис. 2.6) масою m1=20кг прив’язаний трос, який перекинутий через нерухомий блок 4 і другий кінець якого закріплений на поверхні шківа 2 радіусом

До вантажу 1 (рис. 2.6) масою m₁=20кг прив’язаний трос, який перекинутий через нерухомий блок 4 і другий кінець якого закріплений на поверхні шківа 2 радіусом r₂ (m₂=2кг). Механічна система приводиться до руху моментом 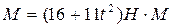прикладеним до ступінчатого шківа 3 масою m₃=3кг.

Знайти закон руху вантажу 1, якщо на тіло 2 діє момент опору М_ОП = 15 Н×м і при t=0 кутова швидкість тіла 3 - 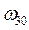= 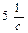. Більший радіус у шківа 2, R₂=0,4м, менший – r₂ = 0,2м, радіус інерції – і₂=0,3м. Тіла 3 та 4 мають однакові маси m₃=m₄ і розміри R₃=R₄=0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.

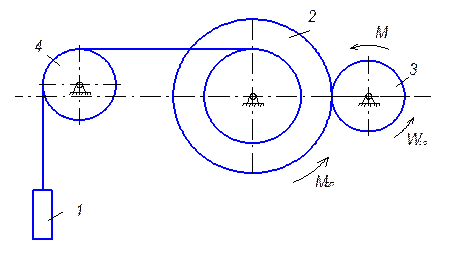
Рисунок 2.6

Розв’язання. Розглянемо окремо рух тіл 2 і 3 та рух тіл 1 і 4.

До тіла 3 (рис. 2.7) прикладені зовнішні сили: пара сил з моментом М, сила тяжіння P₃=m₃g, реакції циліндричного шарніра X₃ і Y₃, реакції тіла 2 – колове зусилля S₃ і сила нормального тиску N₃.

Запишемо диференціальне рівняння обертання тіла 3 навколо нерухомої осі враховуючи, що якщо момент зовнішніх сил діє у напрямку руху тіла, тоді записуємо його з додатним знаком.

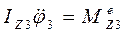
де 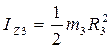- момент інерції тіла відносно осі z, 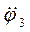- кутове прискорення тіла 3, 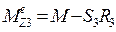- момент зовнішніх сил, прикладених до тіла 3, відносно осі z.

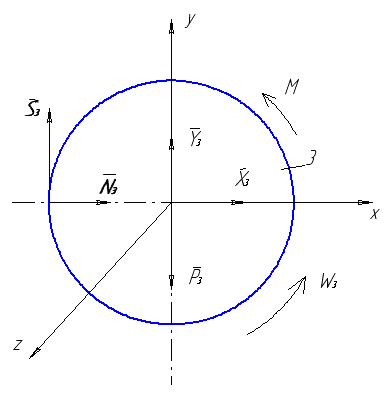
Рисунок 2.7

. (2.1)

Початкові умови:

при t=0, 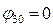, 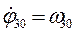. (2.2)

На тіло 2 діють такі зовнішні сили: сила тяжіння P₂=m₂g, реакції циліндричного шарніра X₂ та Y₂, натяг троса S₂ (трос працює тільки на розтяг), реакції тіла 3 – 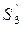та 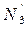, які за третім законом Ньютона направлені в протилежні сторони сил S₃ та N₃ (рис. 2.7).

Диференціальне рівняння обертання тіла 2 (рис. 2.8) навколо горизонтальної осі Z.

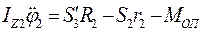(2.3)

де 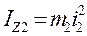- момент інерції тіла 2 відносно осі Z.

Оскільки 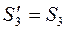, то рівняння (2.3) запишеться у вигляді

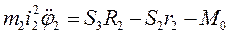(2.4)

До тіл 1 та 4 (рис. 2.9) прикладені зовнішні сили: сили тяжіння P₁=m₁g та P₄=m₄g, реакція троса 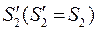, реакції циліндричного шарніра X₄ та Y₄.

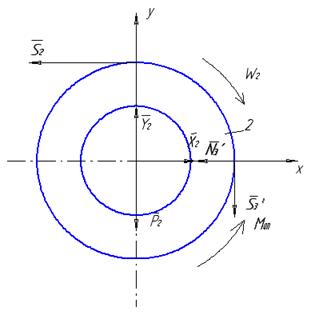
Рисунок 2.8

Теорема про зміну кінетичного моменту для тіл 1 та 4 (рис. 2.9) в проекціях на вісь Z запишеться:

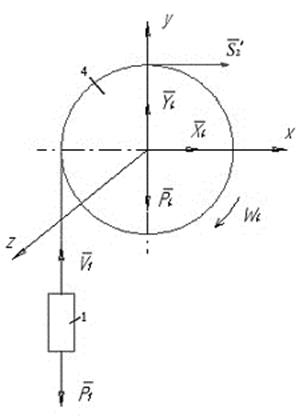
Рисунок 2.9

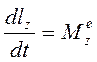(2.7)

де l_Z – кінетичний момент системи тіл 1 та 4 відносно осі Z, 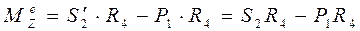- головний момент зовнішніх сил.

Кінетичний момент L_Z складається із моменту кількості руху L_Z1 тіла 1 та кінетичного моменту L_Z4 тіла 4 відносно осі Z

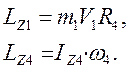
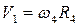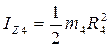Враховуючи, що , а ,кінетичний момент системи L_Z визначимо за формулою

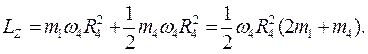
Тепер диференціальне рівняння (2.7) набуває вигляду

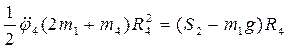(2.8)

Якщо до диференціальних рівнянь (2.1), (2.4), (2.8) додати кінематичні співвідношення

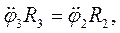
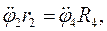
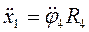(2.9)

тоді отримаємо систему шести рівнянь в які входять невідомі: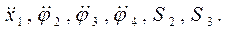

Розв’язуючи систему рівнянь (2.1), (2.4), (2.8), (2.9) маємо:

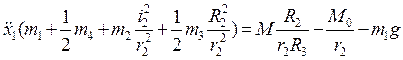
З урахуванням того, що m₁=20кг, m₂=2кг, m₃=m₄=3кг, r₂=0,2м, R₂=0,4м, і₂=0,3м, R₃=R₄=0,3м, М=(16+11t²) 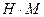, M₀=15 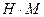, g=9,81 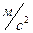, отримаємо

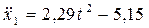. (2.20)

Для визначення закону руху тіла 1, інтегруємо двічи диференціальне рівняння (2.20), беручи до уваги початкові умови (2.2)

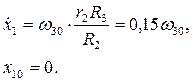
Перший інтеграл диференціального рівняння (2.20)

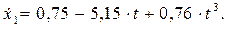
Закон руху тіла 1: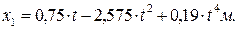

Date: 2015-09-03; view: 403; Нарушение авторских прав