Розв’язування

Система має один ступінь вільності, рівновага – стійка. На систему діють тільки потенціальні сили (сили ваги і пружна сила). Виведемо систему із стану рівноваги. Виберемо за узагальнену координату кут 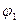відхилення стержня 1 від вертикалі, вважаючи його малим (рис.Д7.б). Тобто маємо 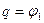і 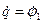. Запишемо рівняння Лагранжа II роду:

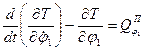(7.1)

Визначимо кінетичну енергію системи, як суму енергій тіл системи. Враховуючи, що стержень 1 обертається навколо нерухомої осі 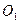, диск 2 - навколо нерухомої осі 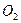, а тіло 3 - рухається поступально, маємо:

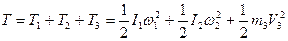, (7.2)

де моменти інерції однорідного стержня 1 довжиною 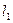і шківа 2 (маса розподілена на ободі) відповідно дорівнюють:

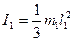, (7.3)

Виразимо швидкості, що входять в (7.2) через узагальнену швидкість :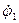

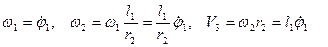(7.4)

Підставимо (7.3) і (7.4) у вираз (7.2):

(7.5)

Кінетична енергія залежить тільки від узагальненої швидкості 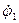. Визначимо похідні, що входять в ліву частину рівняння (7.1):

(7.6)

2. Визначимо узагальнену потенціальну силу, яка відповідає узагальненій координаті , за формулою:

(7.7)

Зобразимо діючі на систему сили та . Задамо системі можливе переміщення, при якому узагальнена координата 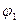зростає, тобто >0, та покажемо можливі переміщення кожного з тіл: для тіла 2 – поворот на кут 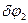, для вантажу 3 – переміщення 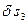. Для визначення узагальненої потенціальної сили обчислимо суму можливих робіт сил на цьому можливому переміщенні системи:

(7.8)

Можливу роботу сили ваги замінимо можливою роботою моменту сили ваги відносно точки О₁, тобто:

,

бо плече між лінією дії сили і точкою дорівнює .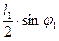

Для сил і відповідно маємо:

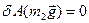, бо точка прикладення сили 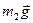нерухома;

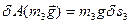, бо кут між силою 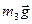і дорівнює нулю.

Можливу роботу пружної сили замінимо можливою роботою моменту пружної сили відносно точки О₁, тобто

, бо плече між лінією дії сили і точкою дорівнює .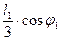

Величина пружної сили залежить від деформації пружини:

,

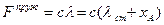де статична деформація пружини (в положенні рівноваги), деформація пружини, коли систему вивели із стану рівноваги.

Враховуючи (7.4), виразимо можливе переміщення вантажу через узагальнене можливе переміщення , а деформацію через узагальнену координату :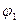

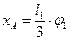; (7.9)

Підставимо (7.8) і (7.9) в формулу (7.7) та отримаємо узагальнену потенціальну силу у вигляді:

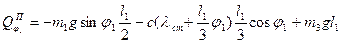(7.10)

Коливання малі, тому можна вважати 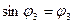, 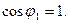Розкриємо дужки і будемо мати:

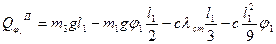(7.11)

В положенні рівноваги (при 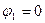) узагальнена потенціальна сила 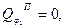тобто:

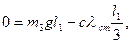(7.12)

звідси знайдемо статичну деформацію :

Таким чином, узагальнена потенціальна сила, враховуючи (7.12), остаточно буде мати вигляд:

(7.13)

3. Складемо рівняння Лагранжа II роду. Підставимо (7.6) і (7.13) в рівняння (7.1):

(7.14)

Запишемо диференціальне рівняння малих вільних коливань у вигляді:

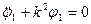, тобто 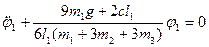(7.15)

Підставимо числові значення, та знайдемо:

,

звідки кругова частота малих вільних коливань 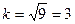(с^-1),

а період коливань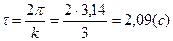

Відповідь: .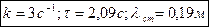

Date: 2015-09-03; view: 284; Нарушение авторских прав