Определение собственных форм колебаний

Положение масс при свободном движении системы определяет ее форму в любой момент времени. Всегда можно задать такие началь­ные условия движения системы, чтобы колебания всех масс происхо­дили только с одной частотой из спектра частот. Такие колебания и соответственные им формы называются главными или нормальными.

Обозначим амплитудные значения перемещений масс в главных формах колебаний по направлению инерционных сил I₂ , I₁, I₃ соответственно Y ₂, Y ₁, Y ₃ . Эти неизвестные перемещения должны удовлетворить следующим уравнениям:

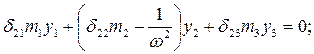(6.9)

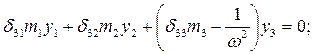
Коэффициенты при неизвестных δ ik ранее найдены, они представляют собой перемещения от инерционных сил. Т. к. полученная системалинейная и однородная, то неизвестные Y ₂, Y ₁, Y ₃ нельзя одно­значно определить. Для нахожденияформы собственных колебаний, соответствующей частоте ω, разделим правые и левые части (6.9) на Y ₁, и введем обозначение отношений ρ:

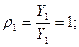
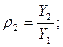
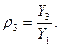(6.10)

Т. к. количество неизвестных значений равно 2, а количест­во уравнений равно 3, то одно из уравнений)6.9) можно отбросить на­пример 3 -е, тогда система примет следующийвид:

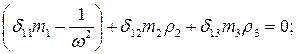(6.11)

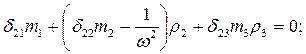
Отсюда для каждой частоты можно определить ρ₁ ρ₂ ρ₃ =1.Рассмотрим случай ω₁ = 0855 сек ^-1. Используя (6.7) уравнения (6.11)перепишем в виде:

(0,994-1,3679)-0,1532 ρ₂+0,432 ρ₃ = 0

-0,0766+(0,4872-1,3679) ρ₂+δ₂₃ т ₃ ρ₃ = 0

Получаем: ρ₂ = - 01157; ρ₃ = 0,802.

Амплитудные значения инерционных сил рис.6.7а определяются следующими формулами:

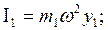
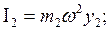
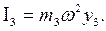
Разделим правые части на силу инерции 1-й массы, т. е. на величину 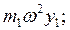и введя обозначения перемещения через ρ (рис. 6.7,б), построим вид эпюр изгибающих моментов / рис. 7в/. Если ρ отрицательное, то соответствующая ей сила инерции меняет направление (рис. 7,в). На рис. 6.7,г показаны изогнутые оси стержней. Это и есть главная форма, соответствующая частоте ω₁=0,855 сек ^{– 1}.

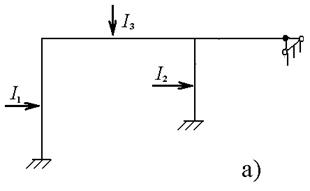
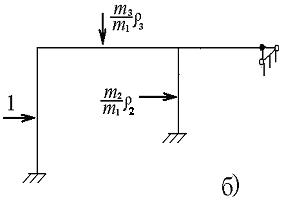
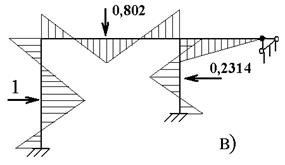
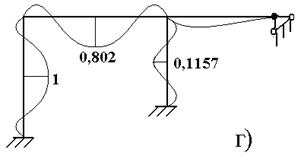
Рисунок 6.7

Аналогично находим главную форму колебаний, соответствующую второй частоте ω₂, т. к. ω₂ = ω₃, то вторая и третья формы будут близки друг к другу, т. е. практически совпадают, берем ω₂ =1,593 сек ^{– 1}, составляем уравнения для ρ:

(0,994-0,394)-0,1532 ρ₂+0,432 ρ₃ = 0;

-0,0766+(0,4872-0,394) ρ₂-0,09 ρ₃ = 0.

Отсюда получаем: ρ₂ = -0,7892; ρ₃ =-1,6688.

На рис. 6.8 указаны приведенные инерционные силы (рис. 6.8,а), вид эпюры изгибающих моментов (рис. 6.8,б), главная форма собственных колебаний, соответствующая ω₂ =1,593 сек ^{– 1} (рис. 6.8,в).

Главные собственные формы должны удовлетворять свойству ортогональности, которые для систем с сосредоточенными массами имеют следующий вид:

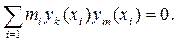
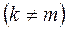
Суммирование ведется по сосредоточенным массам. Ординаты “y” берутся непосредственно под сечениями, где находятся массы из главных форм колебаний. Для нашего случая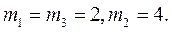

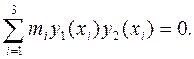
2·11+4·0,7892·0,1157-2·0,802·1,6687=0.

Отсюда вытекает, что найденные главные формы ортогональны.

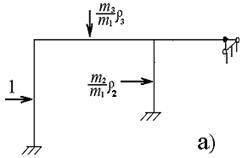
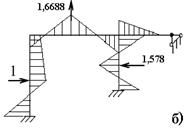
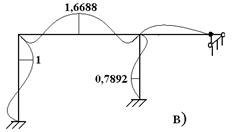
Рисунок 6.8