Динамический расчет плоских рам

I. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим плоскую статически неопределимую раму с располо­женными на ней сосредоточенными массами 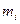. Пренебрегаем собственным весом стержней по сравнению с весом присоединенного груза. На систему действуют вибрационные гармонические нагрузки P_i, которые изменяются в одной фазе и с одинаковой частотой .

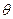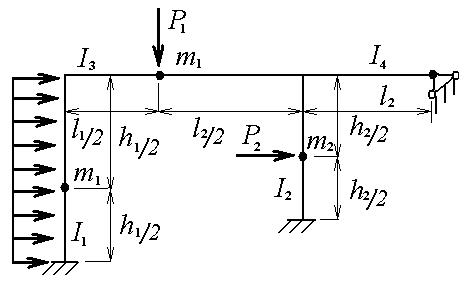
Рисунок 6.1 – Заданная система.

Длины стенок и ригелей имеют следующее величины:

h₁= 4 м; h₂= 3 м; l₁ = 4 м; l₂ = 5 м.

моменты инерции поперечных сечений стержней имеют следующие величины:

; ;

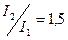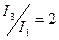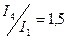
Т.к. внешняя нагрузка – гармоническая, то 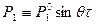; ; 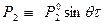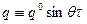, амплитудные значения нагрузок имеют следующие значения: 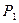=30 кН, 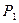=30 кН, 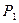=40 кН, q⁰ = 5кН/м.

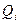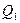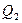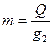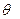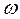Вес масс m_i обозначим , где = 20кН, = 40 кН, массы определяют по формуле: , где g – ускорение свободно падающего тела, g = 9,81 м/сек². Круговая частота колебаний внешней нагрузки равна = 0,6 , где 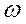- круговая частота собственных системы.

Для динамического расчета необходимо выполнить следующее:

I. Определить динамическую степень свободы, указать направление

инерционных сил.

2. Записать вековое уравнение, определить спектр собственных частот

поперечных колебаний рамы

3. Определить формы главных или собственных колебаний ракш, построив

соответствующие эпюры изгибающих, моментов от инерционных сил.

4. Построить эпюры изгибающих моментов от амплитудных значений внешней вибрационной нагрузки.

5. Определить амплитудные значения инерционных сил,

6. Построить динамические эпюры изгибающих моментов и поперечных сил.

7. Определить динамический коэффициент .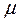

6.1 Определение спектра частот собственных колебаний

Вначале необходимо определить степень свободы заданной системы.

Под степенью динамической свободы понимаем число независи­мых геометрических параметров, определяющих все перемещения в колеблющейся системе. Степень динамической свободы можно определить как минимальное количество добавленных связей, необходимое для закрепления масс от возможных смещений.

Деформации растяжения и сжатия изгибаемых элементов при определении всех возможных перемещений масс не учитываются. Поэтому несколько масс, расположенных на одном стержне рамы, в движении вдоль оси этого стержня ведут себя как одна суммарная масса.

Система на рисунке 1 имеет 3 степени свободы, т.к. необходимо 3 связи для закрепления 3-х масс от всевозможных смещений. На рисунке 2 указаны инерционные силы, вызывающие поперечные колебания стержней.

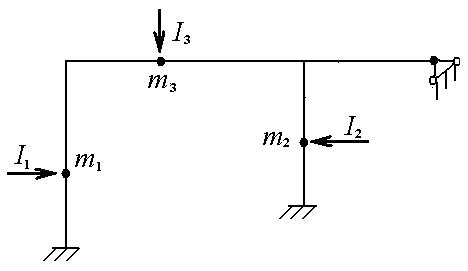
Рисунок 6.2.

Если упругая система в результате взаимодействия с каким-либо другим физическим телом оказывается выведенной из равновесия, то после прекращения указанного взаимодействия система будет совершать свободные колебания с частотой 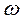. Число возможных свободных колебаний упругой системы равно числу степеней ее свободы. Каждой форме колебаний соответствует своя часто­та 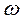. Совокупность частот данной системы составляет ее спектр частот. Для системы рис.1 спектр частот состоит из 3-х частот:

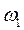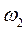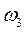, , . Для практических целей часто бывает достаточно най­ти наименьшую частоту 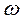_min представляющую наибольшую опасность в смысле возможности возникновения резонанса с вибрационной наг­рузкой. Дело в том, что, во-первых, резонанс на низшей частоте приво­дит к наибольшему динамическому эффекту. Во-вторых, если даже частота возмущающей силы значительно превышает низшую частоту собственных колебаний системе, то резонанс на этой частоте все же будет возникать при разгоне машины во время пуска. Поэтому низшую частоту иногда называют частотой основного тона колебаний. Следующий по порядку тон колебаний называют первым обертоном.

Вековое уравнение

Свободные периодические колебания, совершаемые по гармоническому закону с одной частотой, когда отношение перемещений двух любых точек в любой момент времени не меняется, называются собственными, а соответствующие им частоты называются собственными или главными. Для определения собственных частот 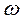составляем характеристическое (векторное) уравнение (6.1). После раскрытия определителя уравнение (6.1) представляет собой кубическое уравнение относительно величины 1/ 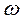². Каждая из инерционных сил приложена к соответствующей массе (рисунок 6.2). Силы инерции I₁ и I₃ приложены к массам, имеющим одинаковые значения, поэтому m₃ = m₁

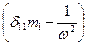
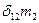
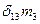
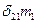
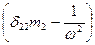
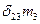= 0 (6.I)

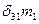
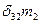
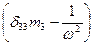
В уравнении (6.1) 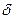_ис представляет собой статическое перемещение по направлению ^“ i” инерционной силы, вызванное единичным значением "k" инерционной силы. Для симметричных систем с сим­метрично расположенными массаж возможны прямо симметричные и об­ратно симметричные формы колебаний, при которых силы инерции соответственно будут прямо симметричны и обратно симметричны. В этом случае перемеще­ния вычисляются как групповые от парных прямо симметричных и обратно симметричных единичных сил. Побочные же перемещения, связы­вающие прямо симметричные и обратно симметричные силы инерции, обращаются в нуль. Это так же приводит к распаду уравнения частот (6.I) на два независимых уравнения, из которых одно позволит найти частоты симметричных колебанийдругое - обратно симметричных.

При этом т.к. групповые перемещения находятся от парных единич­ных сил, то соответствующая масса должна входить в вековое урав­нение с коэффициентом ½. Сами массы определяются через вес:

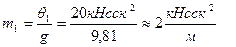
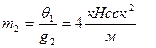
Перемещения от единичных сия вычисляются с помощью интегралов Мора путем перемножения построенных от них эпюр изгибающих моментов M₁, М₂, М₃. Каждая из этих эпюр строится статическим путем от единичного значения соответствующей инерционной силы I = I. Т.к. заданная рама статически неопределима, то для построения эпюр М₁, M₂, М₃ необходимо использовать метод сил или метод перемещений. В данном случае удобно использовать метод перемеще­ний. Построим эпюру M₁ от I₁ =I. На рис. 6.3 а, указала основная система метода перемещений, единичные и грузовые эпюры представ­лены на рис. 6.3 б, рис. 6.3 в, рис. 6.3 г.

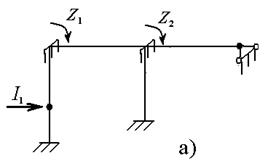
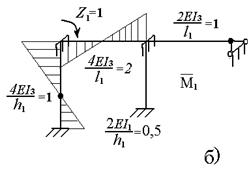
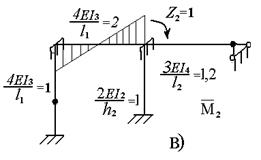
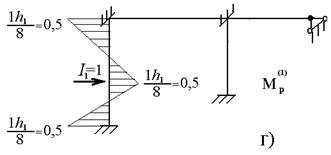
Рисунок 6. 3

Канонические уравнения метода перемещений для случая 2-х неизвестных Z₁, Z₂ имеют вид:

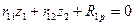
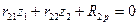(6. 2)

Коэффициенты и грузовые плены уравнений (6.2) определяютсяизэпюр, представленных на рис.6.3, статическим путем. Вырезая 1-й узелиз эпюры М, и рассматривая его равновесие, находим, что 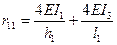.Из этой же эпюры, вылезая второй узел и рассматривая его равновесие, находим, что 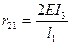. Аналогично из эпюры М₂ находим, что

,

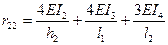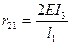
из грузовой эпюры 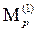определяем грузовой коэффициент ; .

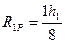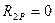Так как заданы отношения моментов инерции поперечных сечений стержней, то для упрощения дальнейших расчетов полагаем: EI₁=1; EI₂=1,5; EI₃=2; EI₄=2. Подставляя значения длин стержней получаем:

;

; ; .

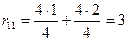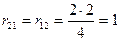
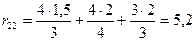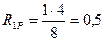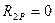Уравнения (6.2) можно переписать в виде:

3Z₁+Z₂+0,5=0; Z₁+5,2Z₂=0. (6.3)

Решая /3/, получаем Z₁= - 0,178, Z₂= 0,034. Окончательная эпюра М₁ от единичной инерционной силы I₁=1 строится путем суммирования

М₁=М₁Z₁+M₂Z₂ +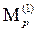

Эпюра M₁ представлена на рисунке 5 а. аналогично строится эпюра М₂ от I=1 и эпюра М₃ от I₃=1. Канонические уравнения имеют вид (6.2), коэффициенты при Z₁ и Z₂ остаются прежними, отличаются только грузовые члены. На рис. 4 а представлена грузовая эпюра от I₂=1, а на рис. 6.4 б грузовая эпюра от I₃=1.

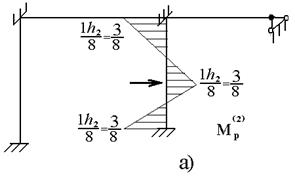
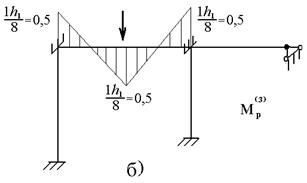
Рисунок 6.4

Соответственно грузовые члены для случая /а/ равны:

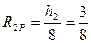; . Канонические уравнения имеют вид:

3Z₁+Z₂=0; Z₁+5,2Z₂+3/8=0. (6.4)

Соответственно получаем Z₁=0,025; Z₂= - 0,075.0кончательно эпюра

М₂ от единичной инерционной силы I₂=1 определяем суммированием:

М₂=М₁Z₁+M₂Z₂ + 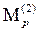= М₁0,025 - M₂0,075 +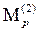

Эпюра М₂ представлена на рис. 6.5, б.

Из рис.6. 4 б определяем:

; .

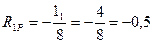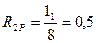Канонические уравнения имеют вид:

3Z₁+Z₂ - 0,5=0; Z₁+5,2Z₂+0,5=0. (6.5)

Решая эту систему, получаем: Z₁=0,212; Z₂= - 0,136. Эпюра М₃ от единичной статически приложенной инерционной силы I₃=1 определяем так же суммированием:

М₃=М₁Z₁+M₂Z₂ + 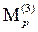= М₁0,212 - M₂0,136 +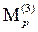

Эпюра М₃ представлена на рис. 6.5, в.

Перемещения δ₁₁, δ₁₂= δ₂₁, δ₁₃= δ₃₁, δ₂₃= δ₃₂, δ₂₂, δ_23. можно определить путем соответствующего перемещения эпюр М₁, М₂, М₃ не между собой а с эпюрами 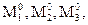построенными для основных систем метода сил и показателями на рис. 6.5.

И так, коэффициенты δ_1К, векового уравнения (6.1) определяется по следующим формулам:

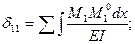
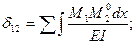
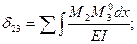
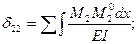
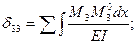
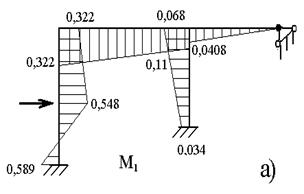
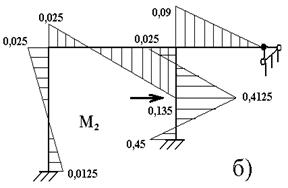
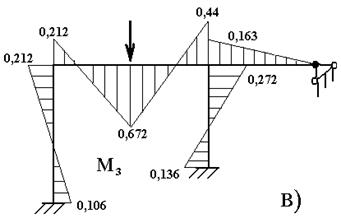
Рисунок 6.5

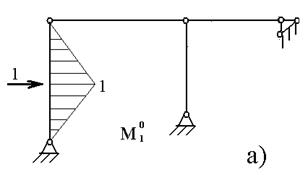
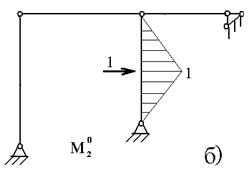
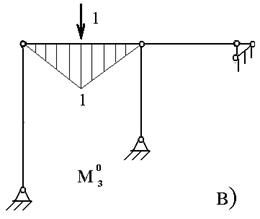
Рисунок 6.6

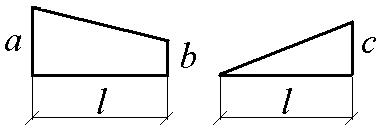
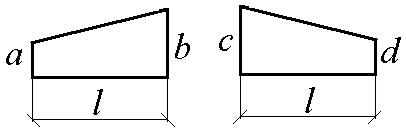
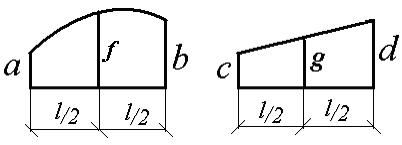
При вычислении интегралов на каждом участке можно воспользоваться таблицей 6.1.

Таблица 6.1

Эпюры М, М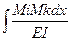

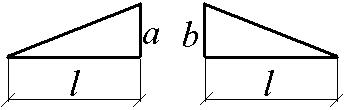
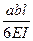
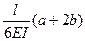
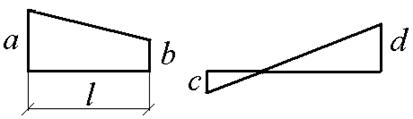
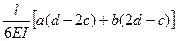
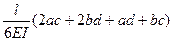
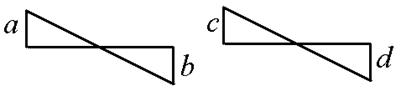
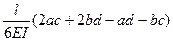
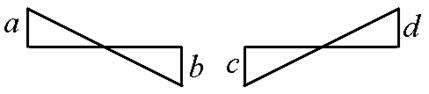
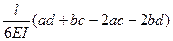
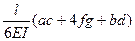
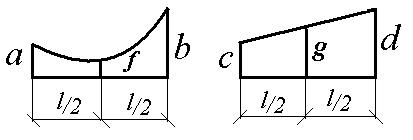
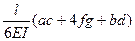
И так, коэффициенты δ_1К, векового уравнения (6.1) определяется по следующим формулам:

δ₁₁=0,497; δ₂₃= - 0,045; δ₁₂= - 0,0383; δ₁₃=0,216; δ₃₃=0,3393; δ₂₂= 0,1218.

Подставляя полученные значения перемещений в уравнение (6.1), получаем:

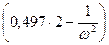
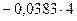
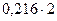
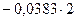
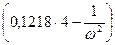
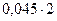= 0 (6.6)

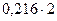
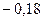
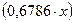
Обозначим 1/ω² = Х, тогда определитель можно переписать в виде:

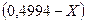
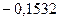
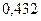
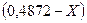
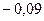= 0 /7/

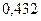
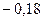
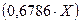
Раскрываем определитель:

(0,994·Х)[(0,4872·Х)(0,6786·Х)-0,18·0,09]+

+0,1532·[0,0766(0,6786·Х)+0,432·0,09]+

+0,432[0,0766·0,18-0,432(0,4872·Х)]=0.

Приведя дробные члены, получаем кубическое уравнение относительно Х:

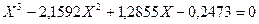
Корни кубического уравнения можно определить по формуле, предварительно сделав замену:

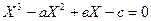Х=У- а/3

и приведя к виду:

у³+ру+q=0 р=в-(а²/3) q=2/27а³-1/3ав+с

для нашего случая имеем:

а = - 2,1598; в = 1,2855; с = - 0,2473; р = - 0,2694; q = - 0,068.

Дискриминант определяется по следующей формуле:

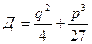
Если Д >0, уравнение имеет один действительный и два сопряженных комплексных корня.

Если Д=0 уравнение имеет 3 действительных корня, из которых два равны.

Если Д <0, уравнение имеет 3 действительных корня. Если Д>0, действительный корень определяется по формуле:

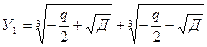
Если Д = 0, то

;

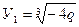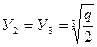
Если Д<0, то

; ;

; ;

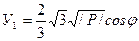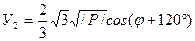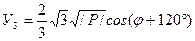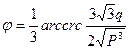Для нашего случая Д=0, поэтому тридействительных корня соответственно равны: 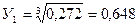; 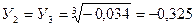. Переходя к X, получаем:

; .

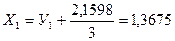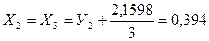Частоты собственных колебаний определяются по формуле:

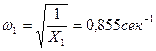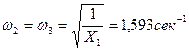; (6.8)

Вообще-то говоря, частоты собственныхколебаний не должны coвпадать, но ввиду их малых значений они могут быть близкидруг к

другу, поэтому можно положить ω₂ ~ ω₃. Из них ω_min = ω₁. =0.855 cек ^-1.

И так, спектр собственных частот найден .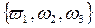

Date: 2015-09-03; view: 4726; Нарушение авторских прав