Потенциальная энергия материальной точки

Для вычисления работы силы на каком либо перемещении в общем случае необходимо знать закон движения точки ее приложения на этом перемещении. Существует особый класс сил, работа которых не зависит от характера движения точки их приложения. Работа таких сил зависит только от начального и конечного положения точки. Такие силы называются потенциальными. К потенциальным силам относится сила тяжести и линейная сила упругости.

Для случая, когда на материальную точку или механическую систему действует только потенциальные силы, вводят понятие силового поля. Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определенная сила, зависящая от координат точки. Силовое поле называют стационарным, если действующие силы не изменяются с течением времени.

Одной из важнейших характеристик силового поля является потенциальная энергия. Она характеризует запас энергии в рассматриваемой точке поля.

Потенциальная энергия П материальной точки в рассматриваемой точке силового поля 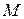- это работа, которую совершают силы поля, действующие на материальную точку при её перемещении из текущего положения 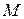в начальное положение .

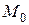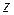
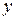
Рис. 28. Потенциальная энергия материальной точки

Рассмотрим материальную точку, перемещающуюся из начального положения в текущее положение . По определению потенциальной энергии получим

, (5.1)

, (5.2)

где 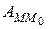- работа сил поля при перемещении точки из текущего положения в начальное ,

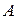- работа сил поля при перемещении точки из начального положения в текущее .

Проекции потенциальной силы, действующей на материальную точку на оси координат можно определить по формулам

;

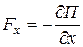; (5.3)

.

Очевидно, что потенциальная энергия определяется с точностью до некоторой постоянной, которая зависит от выбора начальной точки. Эта постоянная не влияет на вычисляемые через потенциальную энергию силы.

Работа потенциальных сил может быть определена по формуле

, (5.4)

где 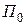потенциальная энергия в начальном положении .

Если за начальную точку выбрать нулевую потенциальную энергию, то есть 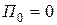, то выражение (5.4) примет вид (5.2).

Если материальная точка находится в действии поля сил тяжести, то, учитывая формулы (4.43) и (5.2) для потенциальной энергии поля сил тяжести, получим

, (5.5)

где 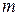- масса материальной точки,

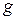- ускорение свободного падения,

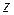- координата точки в текущем положении,

- координата точки в положении принятом за начальное (нулевое).

Обозначим

.

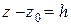Тогда для потенциальной энергии, получим

. (5.6)

Используя формулы (5.3), определим проекции силы тяжести на оси координат:

;

;

.

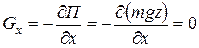Определим потенциальную энергию линейной силы упругости.

Рассмотрим силовое поле линейной силы упругости, подчиняющейся закону Гука:

.

Пусть точка статического равновесия О является началом системы координат (рис. 29).

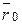
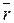
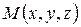
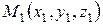
O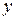

Рис. 29. Потенциальная энергия линейной силы упругости

Определим проекции силы на координатные оси,

,

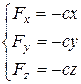где с – коэффициент жесткости,

x,y,z – координаты движущейся точки.

Определим элементарную работу, используя выражение (4.33)

.

Из аналитической геометрии известно:

,

где 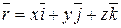- радиус-вектор точки М,

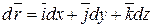- дифференциал радиус-вектора.

Таким образом, элементарная работа определяется по формуле

.

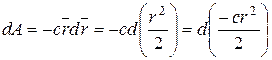Учитывая (5.1), получим

.

Таким образом, потенциальная энергия силы упругости определяется по формуле

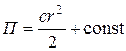. (5.7)

Рассмотрим частные производные от потенциальной энергии по координатам:

;

;

.

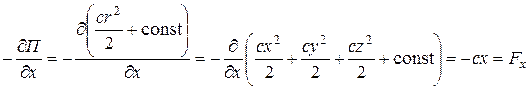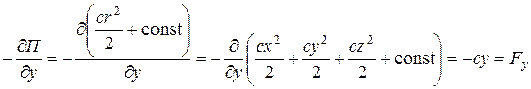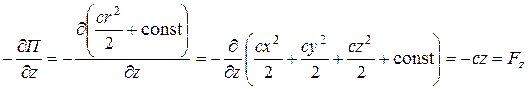Таким образом, для однородного силового поля линейной силы упругости потенциальная энергия определяется формулой (5.7).

2. Потенциальная энергия механической системы

Потенциальной энергией механической системы в рассматриваемом положении 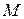потенциального силового поля называется сумма работ сил поля, действующих на систему, которую эти силы совершают при перемещении системы из рассматриваемого положения 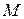в начальное положение .

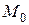Сумму работ потенциальных сил для механической системы можно определить по формуле

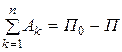, (5.8)

где 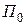- потенциальная энергия системы в ее начальном положении,

- потенциальная энергия системы в ее текущем положении.