Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теорема об изменении кинетической энергии для точки
|
|
Рассмотрим движение материальной точки M массой m, движущуюся со скоростью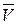 
, под действием силы 
.
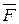Представим основной закон динамики материальной (2.1) точки в виде
.
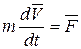Умножив обе части равенства скалярным образом на дифференциал радиус-вектора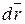 
точки M, получим
.
Рассмотрим правую и левую части этого равенства. Правая часть этого равенства представляет собой элементарную работу силы 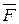, выражаемую по формуле (4.31):
.
Для левой части получим
.
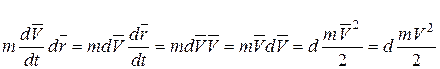Таким образом, окончательно имеем
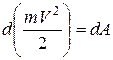. (4.65)
Формула (4.65) выражает теорему об изменении кинетической энергии материальной точки в дифференциальной форме, которую можно сформулировать следующим образом: дифференциал от кинетической энергии материальной точки равен элементарной работе силы, действующей на эту точку.
Разделив (4.65) на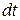 
, получим
. (4.66)
Формула (4.66) выражает вторую формулировку теоремы об изменении кинетической энергии материальной точки в дифференциальной форме. Производная по времени от кинетической энергии материальной точки равна мощности силы, действующей на точку.
Интегрируя выражение (4.65) в соответствующих пределах, получим
, (4.67)
где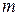 
- масса материальной точки,
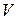- скорость точки в момент времени, когда она занимает положение 
,
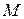- скорость точки в начальный момент времени, когда она занимает положение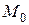 
,
- полная работа силы, действующей на точку при её перемещении из начального положения M 0 в конечное М, определяемая по формуле (4.36)
.
Формула (4.67) выражает теорему об изменении кинетической энергии в интегральной (конечной) форме, которая формулируется следующим образом: изменение кинетической энергии точки, на каком-либо её конечном перемещении равно полной работе силы, действующей на точку на этом же перемещении.
Date: 2015-09-03; view: 420; Нарушение авторских прав