Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Для механической системы
|
|
Рассмотрим механическую систему, состоящую из n точек. Обозначим равнодействующую внешних сил, приложенных к произвольной точке системы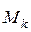 
, как 
, а равнодействующую внутренних сил как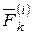 
. Массу точки обозначим 
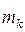, а скорость - 
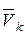. По теореме об изменении кинетической энергии для каждой точки системы (4.65), получим
,
где k = 1,2,3,…, n.
Суммируя, правые и левые части этого выражения по всем точкам рассматриваемой системы, получим
,
.
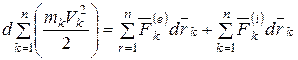Рассмотрим слагаемые, вошедшие в последнее выражение. Первое слагаемое правой части представляет собой сумму элементарных работ всех внешних сил, действующих на все точки системы, то есть
.
Второе слагаемое правой части представляет собой сумму элементарных работ всех внутренних сил, действующих на все точки системы, поэтому
.
Левая часть выражения, учитывая формулу (4.60) 
, представляет собой дифференциал от кинетической энергии, рассматриваемой механической системы. То есть
.
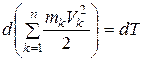Учитывая приведенные выражения, окончательно получим
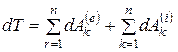. (4.68)
Формула (4.68) выражает теорему об изменении кинетической энергии системы в дифференциальной форме. Эта теорема формулируется следующим образом: дифференциал от кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.
Интегрируя (4.68) между начальным и конечным положением системы, получим
,
, (4.69)
где 
- кинетическая энергия системы в её начальном положении,
- кинетическая энергия систем в конечном положении,
- полная работа внешней силы , действующей на точку 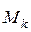при ее перемещении из начального положения 
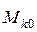в конечное 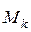, определяемая по формуле
.
- полная работа внутренней силы 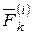, действующей на точку 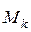при ее перемещении из начального положения 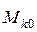в конечное 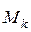, определяемая по формуле
.
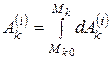Формула (4.69) выражает теорему об изменении кинетической энергии системы в интегральной форме, которая формулируется, следующим образом: изменение кинетической энергии системы при её перемещении из начального положения в конечное равно сумме работ всех внешних и внутренних сил, действующих на систему на этом перемещении.
Если разделить (4.68) на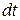 
, получим
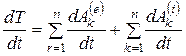
или
. (4.70)
где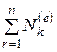 
- сумма мощностей всех внешних сил, действующих на систему,
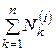- сумма мощностей всех внутренних сил, действующих на систему.
Формула (4.70) выражает теорему об изменении кинетической энергии в дифференциальной форме, формулируемую следующим образом: первая производная по времени от кинетической энергии системы равна сумме мощностей всех внешних и внутренних сил, действующих на систему.
Для механических систем, состоящих из абсолютно твердых тел и абсолютно гибких нерастяжимых нитей, справедливы формулы (4.57), (4.58) и (4.59):
, 
, 
.
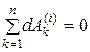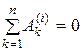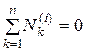Следовательно, для таких механических систем получим
,
,
.
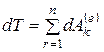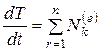Таким образом, для механических систем, состоящих из абсолютно твердых тел и абсолютно гибких нерастяжимых нитей изменение кинетической энергии определяется только внешними силами, действующими на систему.
Date: 2015-09-03; view: 387; Нарушение авторских прав