
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Элементарная работа силы
|
|
Рассмотрим материальную точку М массой m, движущуюся по произвольной траектории со скоростью 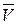 , под действием силы
, под действием силы  (рис. 19).
(рис. 19).

Рис. 19. Движение материальной точки под действием силы 
Введем понятие элементарной работы силы. Элементарной работой силы F на элементарном бесконечно малом перемещении dS называется произведение проекции этой силы на направление скорости на элементарное перемещение. Элементарную работу определяют по формуле
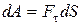 , (4.29)
, (4.29)
где  - проекция силы
- проекция силы 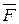 на направление скорости точки ее приложения или на направление элементарного перемещения
на направление скорости точки ее приложения или на направление элементарного перемещения 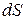 , которое считается направленным по вектору скорости точки
, которое считается направленным по вектору скорости точки 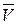 .
.
Элементарная работа является скалярной величиной, и её знак определяется знаком проекции силы  . Если
. Если  > 0, то
> 0, то 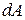 > 0, если
> 0, если  < 0, то
< 0, то 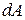 < 0.
< 0.
Обозначим φ угол между вектором силы 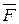 и вектором скорости
и вектором скорости 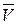 , тогда
, тогда
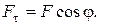
Подставляя 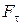 в выражение (4.29), получим
в выражение (4.29), получим
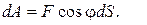 (4.30)
(4.30)
В формуле (4.30) величины F и dS положительны, поэтому если φ < 900, то dA положительна, если 180<φ<90, то dA отрицательна.
Рассмотрим три частных случая:
1. Если 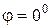 , то
, то 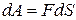 ;
;
2. Если 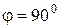 , то
, то 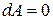 ;
;
3. Если 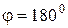 , то
, то 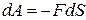 .
.
Таким образом, если сила перпендикулярна к элементарному перемещению (то есть к вектору скорости ее точки приложения) то ее элементарная работа равна нулю.
Из кинематики точки известны следующие соотношения:
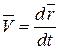 ;
; 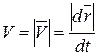 ;
; 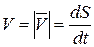 ,
,
Учитывая их, получим
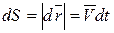 .
.
Подставляя это выражение в формулу (4.30), получим
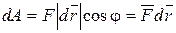 , (4.31)
, (4.31)
где 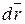 - дифференциал от радиус-вектора точки, считается направленным по касательной.
- дифференциал от радиус-вектора точки, считается направленным по касательной.
Таким образом, элементарной работой силы называют скалярную величину, равную скалярному произведению силы на дифференциал радиус-вектора точки приложения этой силы.
Учитывая, что 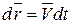 , получим
, получим
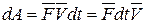 , (4.32)
, (4.32)
где 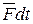 - элементарный импульс силы.
- элементарный импульс силы.
Если силу  и радиус-вектор
и радиус-вектор 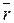 разложить по осям координат, получим
разложить по осям координат, получим
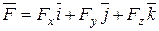 ,
,
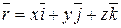 ,
,
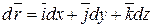 .
.
Подставляя полученные равенства в выражение (4.31), получим аналитическое выражение для элементарной работы силы
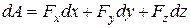 . (4.33)
. (4.33)
Полученное выражение (4.33) называют аналитическим выражением для элементарной работы силы.
Date: 2015-09-03; view: 1627; Нарушение авторских прав