Теорема об изменении кинетического момента для системы

Рассмотрим механическую систему, состоящую из n точек, движущуюся по отношению к инерциальной системе координат Oxyz (рис. 15). Выделим произвольную точку M_k с координатами x_k, y_k, z_k,массой m_k и движущуюся со скоростью 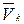. Радиус-вектор этой точки обозначим .

Движение точки происходит под действием внешней силы 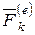и внутренней силы .

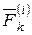Применим теорему об изменении кинетического момента (4.22) для этой точки:

.

Суммируя по всем точкам системы, получим

.

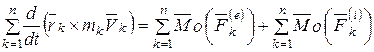
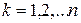Учтем, что

а) ,

где 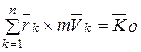- кинетический момент системы относительно центра O (формула (4.19));

б) 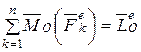- главный момент системы внешних сил;

в) 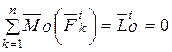- главный момент системы внутренних сил, равный нулю по свойству внутренних сил системы (4.2).

Окончательно получим

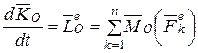. (4.23)

Выражение (4.23) выражает теорему об изменении кинетического момента системы, которую формулируют следующем образом: первая производная по времени от вектора кинетического момента системы относительно произвольно выбранного центра O равна главному моменту внешних сил, действующих на систему, относительно этого же центра.

Проецируя выражения (4.23) на оси координат, получим

,

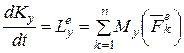, (4.23^/)

,

 

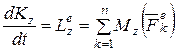где 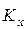, , 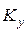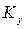- кинетические моменты системы относительно осей координат,

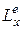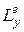, , - проекции главного момента внешних сил системы на координатные оси.

 

 

Date: 2015-09-03; view: 364; Нарушение авторских прав