Дифференциальные уравнения плоского движения твердого тела

Рассмотрим движение твёрдого тела в плоскости Oxy, под действием системы внешних сил 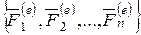. За полюс примем центр масс этого тела точку С (рис. 18).

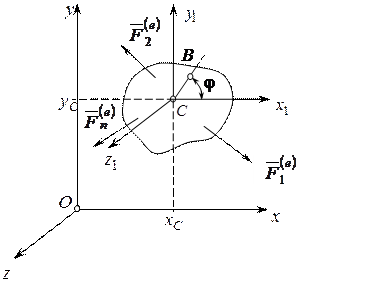
Рис. 18. Плоское движение твердого тела

Введём подвижную систему координат Сx ₁ y ₁ z ₁ в центре масс тела таким образом, чтобы ее оси были параллельны неподвижным осям системы Oxyz.

Плоское движение твёрдого тела рассмотрим как сумму двух движений: движения полюса C (материальной точки) и движения твёрдого тела по отношению к полюсу, которое носит вращательный характер (вращение вокруг подвижной оси Сz ₁).

Положение центра масс системы С по отношению к неподвижным осям определяется координатами .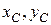

Используя теорему о движении центра масс системы (4.16^/), получим

,

.

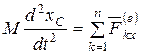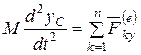Положение произвольной точки B по отношению к полюсу (центру масс C), в любой момент времени характеризуется углом поворота φ, отсчитываемым от положительного направления оси Ox ₁

Используя дифференциальное уравнение вращательного движения твердого тела (4.27), получим

,

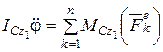где 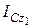- момент инерции твердого тела относительно центральной оси Cz ₁,

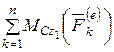- сумма алгебраических моментов внешних сил относительно центральной оси Cz ₁.

Окончательно для твердого тела, совершающего плоское движение (имеющего три степени свободы), получим три дифференциальных уравнения

,

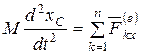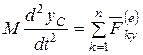, (4.28)

.

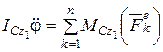Полученные уравнения (4.28) называют дифференциальными уравнениями плоского движения твердого тела.

Date: 2015-09-03; view: 926; Нарушение авторских прав