Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Тела вокруг неподвижной оси
|
|
Рассмотрим твердое тело, вращающееся вокруг неподвижной оси Oz с угловой скоростью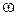 
(рис. 17).
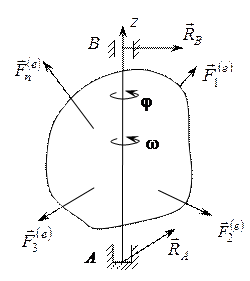
Рис. 17. Вращение твердого тела вокруг неподвижной оси
Из теоремы об изменении кинетического момента (4.23/), имеем
.
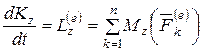При вращении твёрдого тела, вокруг неподвижной оси Oz кинетический момент определяется по формуле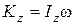 
, учитывая это, получим
.
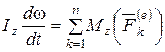Из кинематики твердого тела известна зависимость
,
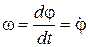где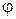 
- угол поворота тела относительно неподвижной оси Oz.
Окончательно получим
,
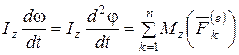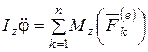. (4.27)
Выражение (4.27) представляет собой дифференциальное уравнение вращения твёрдого тела вокруг неподвижной оси.
Это уравнение полностью аналогично уравнению поступательного движения твердого тела (4.17/). В уравнении (4.27) момент инерции Iz является аналогом массы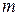 
, 
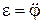играет роль линейного ускорения 
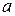, а сумма моментов внешних сил 
играет роль главного вектора внешних сил 
.
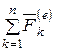Под действием системы внешних сил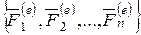 
в подпятнике А и подшипнике В возникнут реакци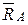и 
и 
, эти реакции тоже являются внешними силами, но их моменты относительно оси вращения Oz равны нулю, так как их линии действия пересекают эту ось, поэтому при составлении дифференциальных уравнений вращательного движения эти реакции можно не учитывать.
Дифференциальное уравнение (4.27) позволяет решать две основные задачи, которые аналогичны первой и второй задачам динамики точки. Рассмотрим формулировки этих задач.
1. Первая задача. По заданному закону вращения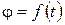 
и известному моменту инерции твердого тела относительно оси вращения 
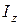требуется определить момент внешних сил относительно этой оси.
2. Вторая задача. По заданным начальным условиям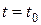 
, 
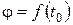и известному моменту внешних сил относительно оси вращения требуется определить закон вращения тела как функцию времени .
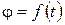Решение первой задачи аналогично решению первой основной задачи динамики материальной точки, решение второй задачи аналогично решению второй основной задачи динамики материальной точки. Методы интегрирования уравнения (4.27) аналогичны методам интегрирования уравнений (2.3/). На первом этапе интегрирования определяется угловая скорость и её зависимость от времени, на втором этапе определяется закон вращения.
Date: 2015-09-03; view: 711; Нарушение авторских прав