
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Интегрирование по частям
|
|
Интегрирование по частям – это, практически, формула интегрирования произведения двух функций.
Хорошо известна формула дифференциала произведения двух функций:

Проинтегрировав обе части данного равенства, получим:
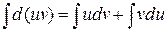 ,
,
т.к.
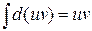 ,
,
то
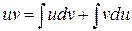 ,
,
откуда
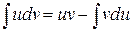 .
.
Последняя формула называется формулой интегрирования по частям.
Формула интегрирования по частям сводит нахождение интеграла  к отысканию другого интеграла
к отысканию другого интеграла 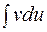 ; её применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо подобен ему.
; её применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо подобен ему.
При этом в качестве 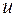 берётся функция, которую проще продифференцировать, а в качестве
берётся функция, которую проще продифференцировать, а в качестве  берётся та часть подынтегрального выражения, которую проще проинтегрировать. Иногда формулу интегрирования по частям приходиться использовать несколько раз.
берётся та часть подынтегрального выражения, которую проще проинтегрировать. Иногда формулу интегрирования по частям приходиться использовать несколько раз.
При применении формулы интегрирования по частям интегралы можно разбить на 3 основные группы:
1. В интегралах вида
 ,
,
где 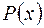 - многочлен переменной
- многочлен переменной  ,
,  - число, полагают
- число, полагают
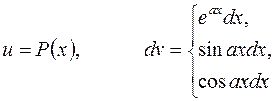
2. В интегралах вида

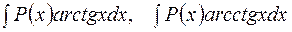
полагают
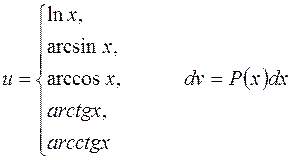
3. В интегралах вида
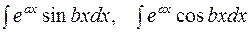
за 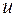 принимают любую функцию, за
принимают любую функцию, за  соответственно оставшуюся часть подынтегрального выражения.
соответственно оставшуюся часть подынтегрального выражения.
Пример 1. Найти  .
.
Решение. Данный интеграл относится к первой группе, поэтому
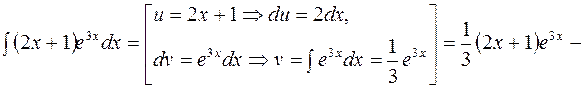
 .
.
Пример 2. Найти  .
.
Решение. Данный интеграл относится ко второй группе, поэтому положим 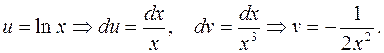
Тогда по формуле интегрирования по частям находим:
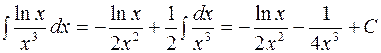 .
.
Пример 3. Найти 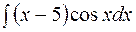 .
.
Данный интеграл относится к первой группе, поэтому 
 , по формуле интегрирования по частям имеем
, по формуле интегрирования по частям имеем
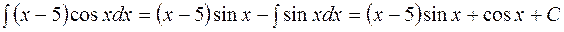 .
.
Пример 4. Найти 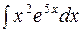 .
.
Решение. Интеграл относится к первой группе, поэтому 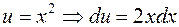 ,
, 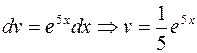 , тогда имеем
, тогда имеем
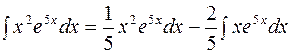 .
.
К последнему интегралу снова применим формулу интегрирования по частям, положив  , тогда получим
, тогда получим
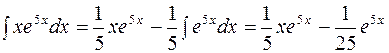 .
.
Исходный интеграл равен
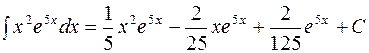 .
.
Пример5. Найти 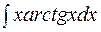 .
.
Решение. Данный интеграл относится ко второй группе, поэтому 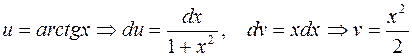 . По формуле интегрирования по частям получим
. По формуле интегрирования по частям получим
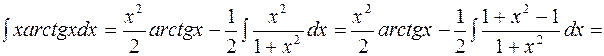
= 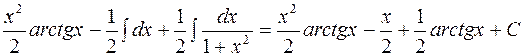 .
.
Пример 6. Найти  .
.
Решение. Данный интеграл относится к третьей группе, поэтому выбор 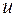 и
и  в данном случае произволен. Пусть
в данном случае произволен. Пусть 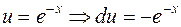 ,
, 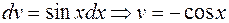 , тогда по формуле интегрирования по частям получим
, тогда по формуле интегрирования по частям получим
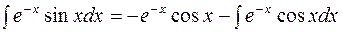 .
.
Для второго интеграла применим ещё раз формулу интегрирования по частям:
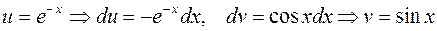 ,
,
тогда
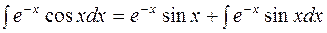 .
.
Подставляя полученное выражение в соотношение для исходного интеграла, получим
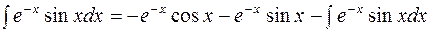 .
.
Перенесём интеграл из правой части в левую, получим
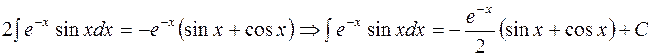
Найти неопределённый интеграл методом интегрирования по частям:
№1.  №2.
№2. 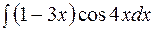
№3. 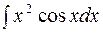 №4.
№4. 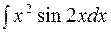
№5. 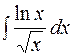 №6.
№6. 
№7. 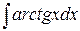 №8
№8 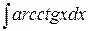
№9. 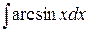 №10.
№10. 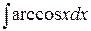
№11. 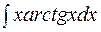 №12.
№12. 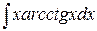
№13.  №14.
№14. 
№15. 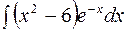 №16.
№16. 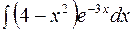
№17.  №18.
№18. 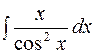
№19. 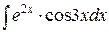 №20.
№20. 
Date: 2015-09-02; view: 408; Нарушение авторских прав