Метод замены переменной (способ подстановки)

Найти заданный неопределённый интеграл непосредственным интегрированием удаётся далеко не всегда, а иногда это сопряжено с большими трудностями. В таких случаях применяют другие способы интегрирования.

Одним из наиболее эффективных методов является способ подстановки или замены переменной интегрирования.

Сущность этого метода заключается в том, что путём введения новой переменной интегрирования удаётся свести заданный интеграл к новому интегралу, который сравнительно лёгко берётся непосредственно.

Алгоритм метода:

Пусть дан интеграл 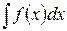, который не является табличным.

1. Записываем уравнение замены

,

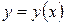где - некоторая функция.

2. Находим дифференциал этой функции

.

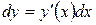3. Выражаем

.

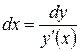4. Подставим 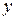и в данный интеграл:

.

Если замена выполнена правильно, то

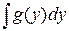
будет табличным.

5. Находим

.

6. Чтобы получить окончательный ответ, вместо переменной 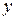подставляем выражение :

.

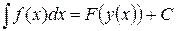Пример 1. Найти .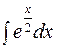

Решение. Сделаем подстановку 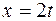, тогда 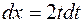. Следовательно,

.

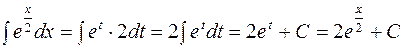Пример 2. Найти .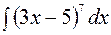

Решение. Сделаем подстановку 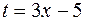, тогда , следовательно,

.

Пример 3. Найти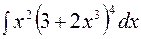

Решение. Сделаем подстановку 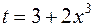, тогда 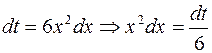, следовательно,

.

Пример 4. Найти .

Решение. Сделаем подстановку 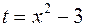, тогда , получаем

.

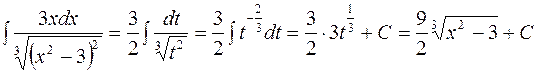Пример 5. Найти .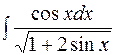

Решение. Подстановка 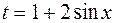, тогда 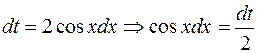, получим

.

Пример 6. Найти .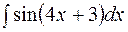

Решение. Сделаем подстановку , тогда , следовательно,

.

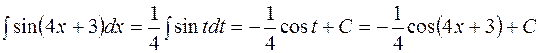Пример 7. Найти .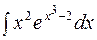

Решение. Сделаем подстановку 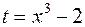, тогда 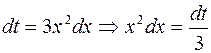, следовательно,

.

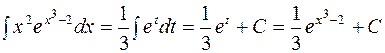Пример 8. Найти .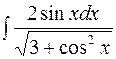

Решение. Сделаем подстановку , тогда 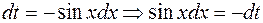, получим

Пример 9. Найти .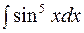

Решение. Преобразуем подынтегральную функцию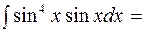

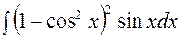= . Сделаем замену , тогда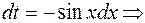

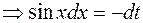, получим

= .

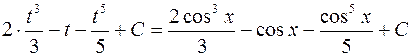Пример 10. Найти .

Решение. Замена 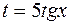, тогда 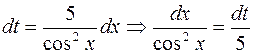, получаем

.

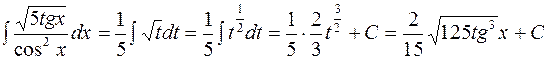Пример 11. Найти .

Решение. Сделаем замену 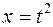, тогда 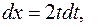получаем

.

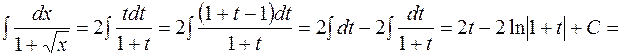
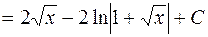Часто при нахождении неопределённых интегралов используются следующая теорема:

,

на основании которой может быть составлена следующая таблица интегралов от сложных функций, промежуточным аргументом которых является линейная функция:

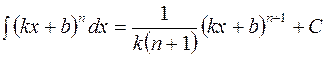
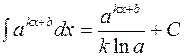
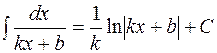
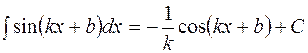
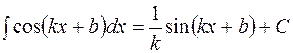
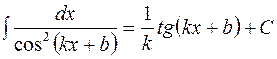
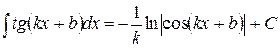
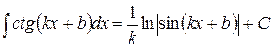
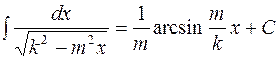
Пользуясь данной таблицей можно в некоторых случаях, не применяя метод замены переменной, сразу получать конечный результат.

Date: 2015-09-02; view: 490; Нарушение авторских прав