
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные теоремы и формулы операционного исчисления
|
|
 2.1. Оригинал и изображение
2.1. Оригинал и изображение
В качестве исходной формулы для дальнейших выводов возьмем формулу
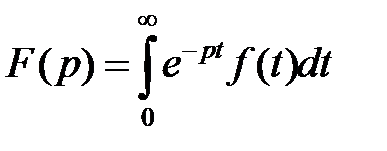 , (2.1)
, (2.1)
определяющую преобразование Лапласа.
Функция 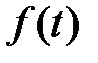 вещественного независимого переменного
вещественного независимого переменного 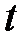 , стоящая в формуле (2.1) под знаком интеграла Лапласа, называется начальной функцией или оригиналом; функция
, стоящая в формуле (2.1) под знаком интеграла Лапласа, называется начальной функцией или оригиналом; функция  комплексного независимого переменного
комплексного независимого переменного 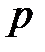 называется изображением функции
называется изображением функции 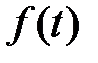 .
.

|

|

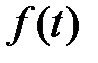 ,
, 
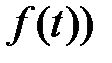 ,
,

|

|
 является оригиналом для функции
является оригиналом для функции  , или формулой
, или формулой

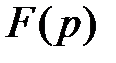 , (
, (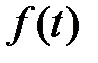
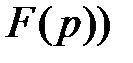 ,
,
показывающей, что функция 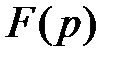 является изображением.
является изображением.
Стрелка в этих символических формулах своим острием всегда должна быть направлена к оригиналу.
Иногда для изображения связи между оригиналом и изображением пользуются символическими формулами


 и
и
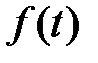
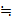
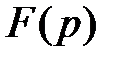 .
.
Изображения имеют только те функции, для которых имеет смысл интеграл Лапласа (2.1).
Примером функции, не имеющей изображения, может служить функция 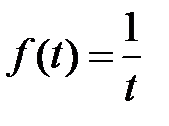 . Точно так же не всякая функция комплексного переменного может рассматриваться как изображение некоторой функции вещественного переменного. Например, не имеет оригинала функция
. Точно так же не всякая функция комплексного переменного может рассматриваться как изображение некоторой функции вещественного переменного. Например, не имеет оригинала функция 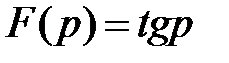 , так как полюсы этой функции распределяются по всей вещественной оси. То есть на плоскости
, так как полюсы этой функции распределяются по всей вещественной оси. То есть на плоскости 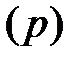 нет ни одной прямой, параллельной мнимой оси, справа от которой эта функция была бы регулярной.
нет ни одной прямой, параллельной мнимой оси, справа от которой эта функция была бы регулярной.
Мы будем рассматривать только такие начальные функции 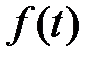 , которые удовлетворяют трем условиям:
, которые удовлетворяют трем условиям:
1) 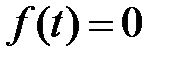 при
при 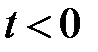 ,
,
2) 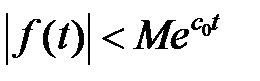 при
при 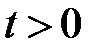 ,
,
где 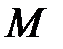 и
и 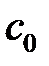 - некоторые положительные постоянные числа,
- некоторые положительные постоянные числа,
3) на любом конечном отрезке 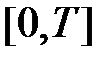 для функции
для функции 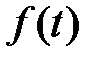 выполняются условия Дирихле.
выполняются условия Дирихле.
Кроме того, всегда будем считать, что в формуле (1)
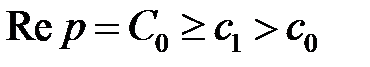 ;
;
при этих условиях интеграл Лапласа, определяющий функцию 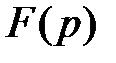 , будет сходиться (и притом равномерно), во всей полуплоскости, ограниченной прямой
, будет сходиться (и притом равномерно), во всей полуплоскости, ограниченной прямой 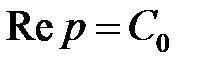 . Функции, удовлетворяющие всем этим условиям, называются «изображенными по Лапласу».
. Функции, удовлетворяющие всем этим условиям, называются «изображенными по Лапласу».
Date: 2015-09-02; view: 457; Нарушение авторских прав