Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Преобразование Лапласа и формула обращения
|
|
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
1.1. Интеграл Фурье
Пусть в промежутке 
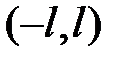функция 
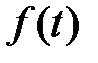удовлетворяет условиям Дирихле, а именно:
а) ограничена на этом отрезке;
б) кусочно-непрерывна на нем (имеет конечное число точек разрыва первого рода);
в) кусочно-монотонная (в частности, имеет лишь конечное число экстремумов).
Тогда, как известно из теории тригонометрических рядов, функция может быть на этом отрезке представлена сходящимся к ней тригонометрическим рядом
. (1.1)
По теореме Дирихле:
1) в точках непрерывности сумма ряда равна значению функции;
2) в точках разрыва сумма ряда равна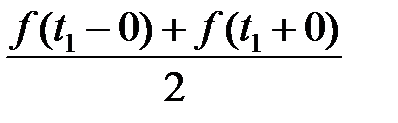 
, а на концах промежутка 
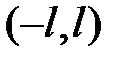, то есть при 
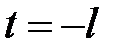и 
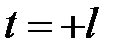равна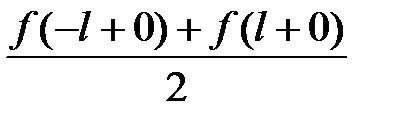 
.
Коэффициенты ряда (1.1) определяются по формулам Эйлера-Фурье:
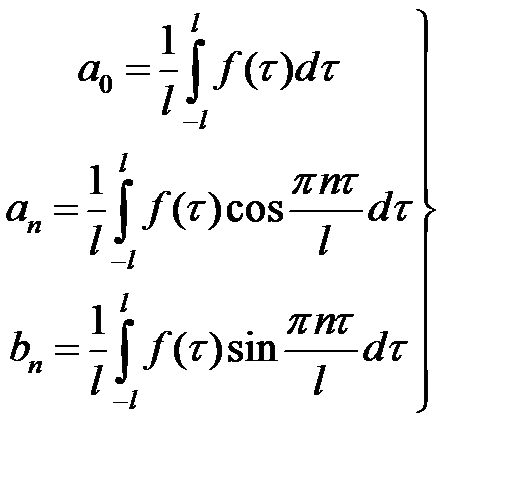(1.2)
Так как косинус есть функция четная, а синус – функция нечетная, то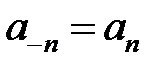 
, 
, формулу (1.1) можно записать в виде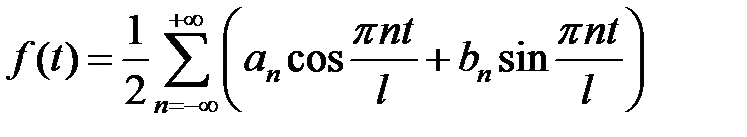 
или, с учетом формул (1.2),
,
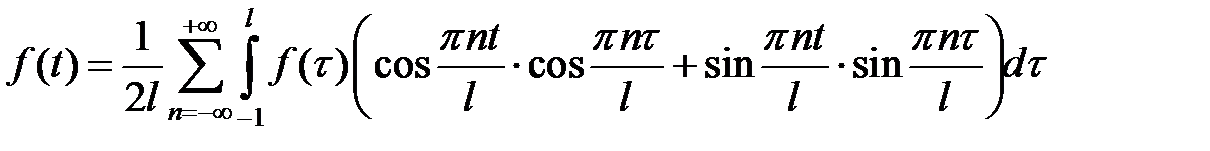откуда
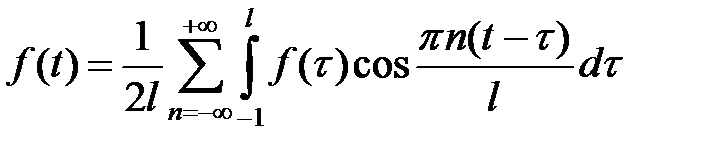. (1.3)
Обозначим
, (1.4)
приведем формулу (1.3) к виду:
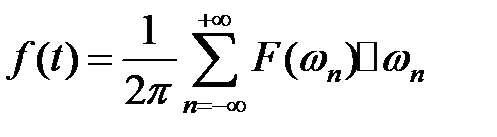. (1.5)
Если в промежутке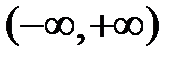 
функция 
абсолютно интегрируема, т.е.
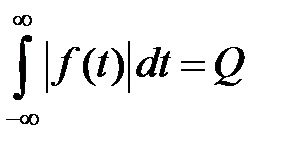, (1.6)
где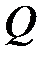 
- конечное число, то переходя в равенстве (1.5) к пределу при 
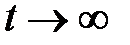и замечая, что 
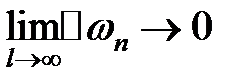, получаем формулу: 
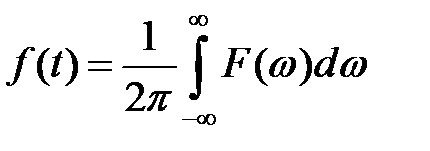, или
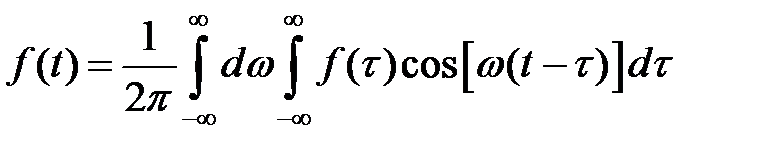. (1.7)
Интеграл, стоящий в правой части равенства (1.7), называется интегралом Фурье.
Замечая, далее, что
(1.8)
(т.к.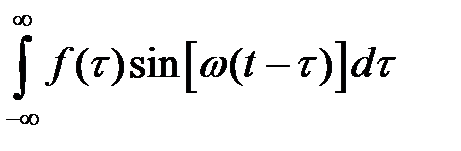 
- является нечетной функцией аргумента 
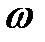) преобразуем формулу (1.7)
,
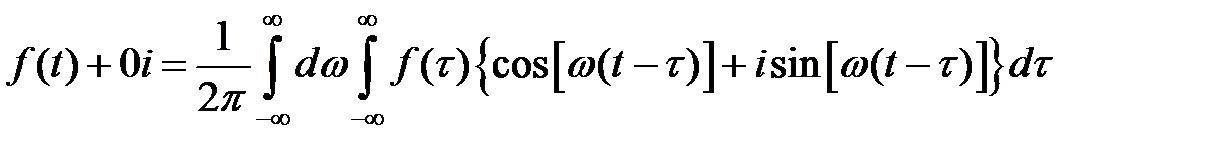откуда
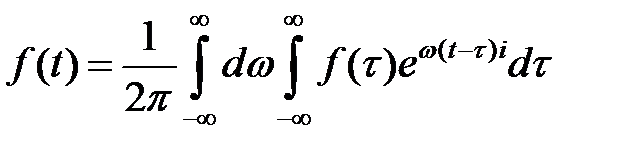. (1.9)
Интеграл, стоящий в правой части формулы (1.9), называется интегралом Фурье в комплексной форме.
1.2. Преобразование Лапласа и формула обращения
Докажем теперь, что если функция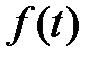 
не интегрируема абсолютно, удовлетворяет условиям:
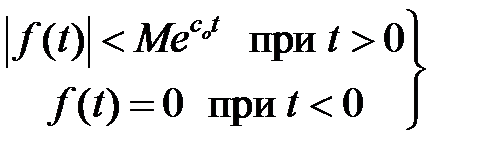, (1.10)
Где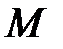 
и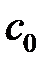 
- некоторые постоянные положительные числа, то при
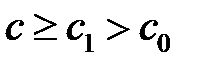(11.10а)
функцию
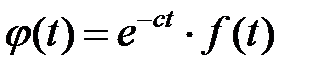(1.10б)
можно представить интегралом Фурье:
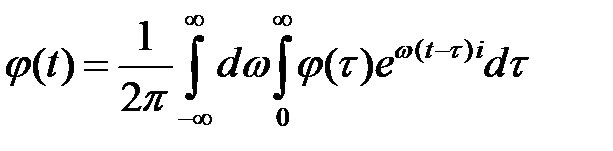. (1.10в)
В самом деле, если условия (1.10) и (1.10а) выполняются, то
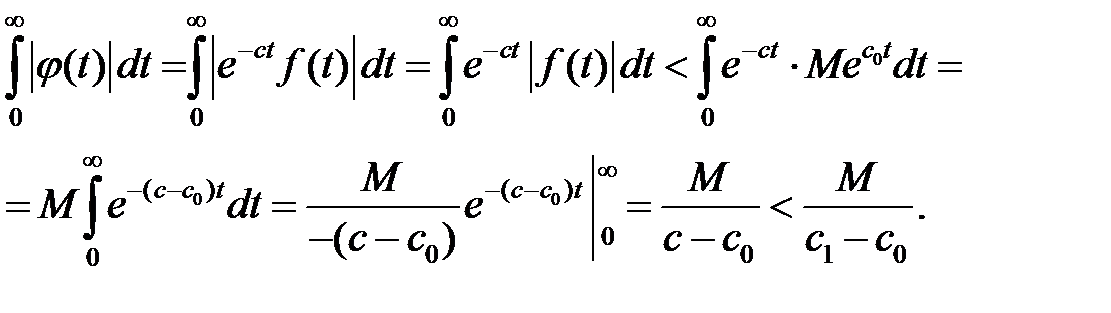
Таким образом, в интервале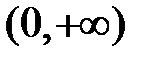 
функция 
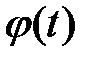оказывается абсолютно интегрируемой, что и доказывает возможность представления ее в этом интервале интегралом Фурье (1.10в).
Заменяя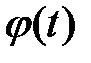 
в равенстве (1.10в) на 
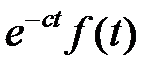(формула (1.10б)):
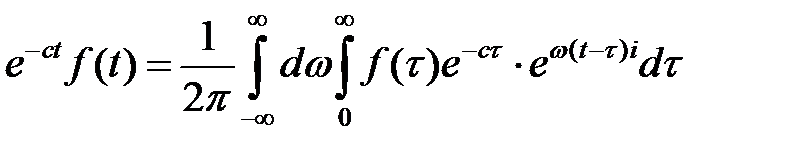
и умножая обе части этого равенства на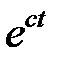 
, получим
,
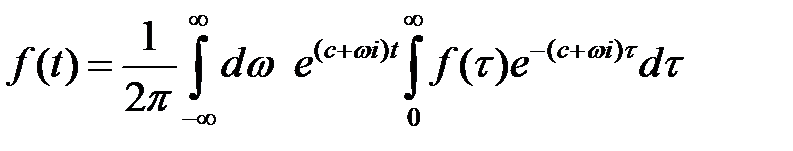обозначим
. (1.11)
Так как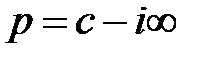 
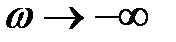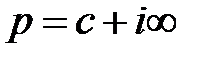при 
; 
при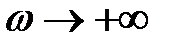 
, то последняя формула для 
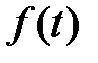принимает вид:
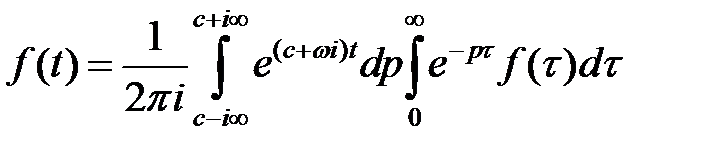, (1.12)
это преобразованный интеграл Фурье.
Если положить:
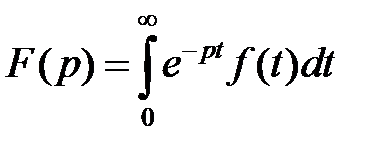, (1.13)
То
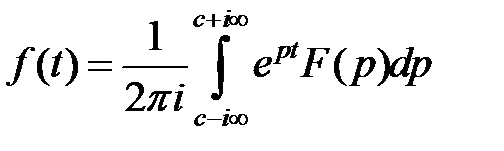. (1.14)
В операционном исчислении формула (1.13) является основной. Формула эта, в правой части которой стоит так называемый интеграл Лапласа, определяет преобразование Лапласа, при помощи которого функция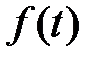 
вещественного независимого переменного 
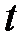преобразуется в функцию 
комплексного независимого переменного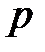 
.
Функцию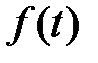 
называют начальной функцией или оригиналом, а функцию 
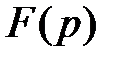, получаемую из 
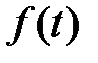при помощи преобразования Лапласа, изображением функции 
.
Легко доказать, что, если функция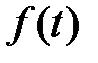 
удовлетворяет условиям Дирихле и условиям (1.10), то изображение 
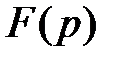представляет собой функцию, регулярную при всех значениях комплексного независимого переменного 
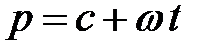, удовлетворяющих неравенствам (1.10а), то есть регулярную по всей полуплоскости, расположенной справа от прямой 
.
|
|
|
|
|
|
|
|
|
|
|
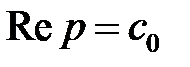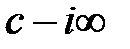
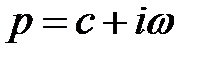
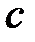
Формула (1.14), в правой части которой стоит так называемый интеграл обращения, определяет преобразование обратное преобразованию Лапласа, то есть преобразование, при помощи которого функция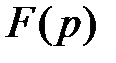 
комплексного переменного 
преобразуется в функцию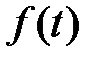 
вещественного независимого переменного 
.
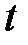Date: 2015-09-02; view: 497; Нарушение авторских прав