Понятие группы

Определение

Множество G на котором определена бинарная операция (*) называется группой (G,*), если выполняются условия:

1. Операция (*) ассоциативна.

2. Для операции существует нейтральный элемент.

3. Все элементы G обратимы.

Примеры групп

1. R - группа действительных чисел с операцией сложения. (аддитивная группа действительных чисел)

2. C - аддитивная группа комплексных чисел.

3. - группа ненулевых действительных чисел с операцией умножения (мультипликативная группа действительных чисел)

4. 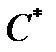- мультипликативная группа комплексных чисел.

5. 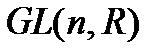- группа невырожденных матриц порядка n с действительными элементами. (Аналогично, )

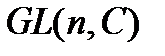6. 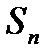- группа перестановок множества 1,2,..., n.

Во всех этих примерах наличие свойств 1- 3 не вызывает сомнений.

Прежде чем приводить другие примеры групп укажем некоторые простейшие свойства этих алгебраических систем. Во всех последующих формулировках считается, что x, y, z,... - элементы некоторой группы G.

1. Закон сокращения

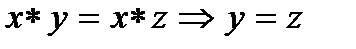(левое сокращение)

(правое сокращение)

Докажем, например, первый закон. Используем существование обратного элемента 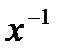и свойство ассоциативности операции.

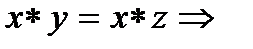
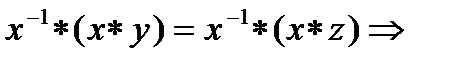
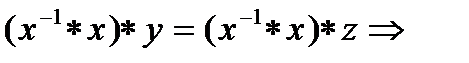
y=z.

2. Единственность нейтрального элемента

В любой группе нейтральный элемент определен однозначно. В самом деле, есл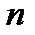и и 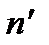оба являются нейтральными, то по определению

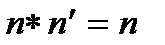и в то же время 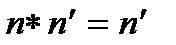, откуда . Единственный нейтральный элемент группы G будет в дальнейшем обозначаться 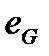или просто e.

3. Единственность обратного элемента

Для каждого элемента x обратный элемент 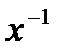определен однозначно. В самом деле, если элементы y и z являются обратными для x, то y*x=e и z*x=e, откуда y*x=z*x и по закону сокращения y=z.

4. Признак нейтрального элемента

Действительно, поскольку 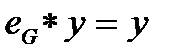, имеем , откуда по закону сокращения получаем .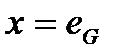

5. Разрешимость любого уравнения первой степени (существование обратной операции)

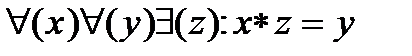. Элемент z определен однозначно. (Его можно назвать «частным» от деления y на x).

Имеем: 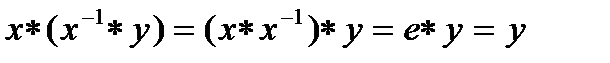и значит можно взять . Однозначность следует из закона сокращения: .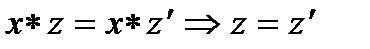

Определение. Непустое множество M называют кольцом, если оно удовлетворяет следующим требованиям:

1. Для элементов этого множества введено отношение равенства.

2. На этом множестве определена внутренняя бинарная операция, называемая сложением, обладающая следующими свойствами:

1) сложение – операция алгебраическая,

2) сложение – операция коммутативная,

3) сложение – операция ассоциативная,

4) относительно неё в множестве M существует нейтральный элемент – «нуль», обозначенный символом Ō,

5) сложение – операция симметризуемая.

3. На этом множестве определена внутренняя бинарная операция, называемая умножением, обладающая следующими свойствами:

1) умножение – операция алгебраическая,

2) умножение – операция ассоциативная,

3) умножение двояко дистрибутивно относительно сложения.

Замечание. В целом умножение в кольце не обязано быть ассоциативным. Т.к. мы изучаем в общем курсе математики только кольца с ассоциативным умножением, то требование ассоциативности умножения принято включать в состав аксиом кольца.

Определение. Кольцо называется коммутативным, если умножение в нём коммутативно. Кольцо называется некоммутативным, если умножение в нём некоммутативно.

Не всякое кольцо содержит нейтральный элемент (единицу) по умножению.

Кольцо называется кольцом с единицей, если относительно умножения в нём существует нейтральный элемент (единица). Если же в кольце нейтрального элемента по умножению нет, то кольцо называется кольцом без единицы.

Примеры колец.

1. Существует кольцо, содержащее лишь один элемент, который неизбежно должен быть нулём. Такое кольцо называется нулевым кольцом. Это коммутативное кольцо с единицей, роль которой играет ноль.

2. Множество Z всех целых чисел относительно обычных операций сложения и умножения есть коммутативное кольцо с единицей, роль которой играет целая рациональная единица.

3. Множество 2 Z всех чётных целых чисел относительно обычных операций сложения и умножения есть коммутативное кольцо без единицы.

4. Множество всех квадратных матриц вида 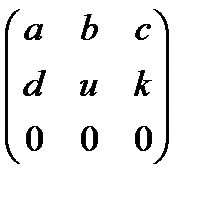с вещественными элементами относительно обычных операций сложения и умножения матриц есть некоммутативное кольцо без единицы. Это кольцо содержит бесконечно много левых единиц, которыми являются матрицы вида , где x и y – любые вещественные числа, но не имеет правой единицы.

5. Множество всех квадратных матриц вида 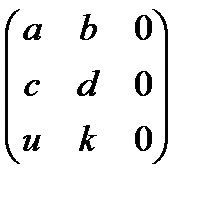с вещественными элементами относительно обычных операций есть некоммутативное кольцо без единицы. Это кольцо содержит бесконечно много правых единиц, которыми являются матрицы вида , где x и y – любые вещественные числа, но не имеют левой единицы.

Понятие поле. Особый тип колец с единицей представляют собой поля. При этом ноль кольца и его единица предполагаются различными. Другими словами, в поле должно быть по крайней мере два элемента.

Определение. Полем называется кольцо

1) коммутативное,

2) с единицей,

3) каждый, отличный от нуля элемент которого обратим.

Из определения следует, что всякое поле должно быть кольцом, но не всякое кольцо обязано быть полем.

Примеры полей:

1. Поле рациональных чисел.

2. Поле вещественных чисел.

3. Поле комплексных чисел

4. Поле Z ₅.

Для поля всегда справедливы следующие утверждения:

1. В поле всегда разрешимы уравнения

ax = b, где a ≠ 0;

ya = b, где a ≠ 0, причем однозначно.

2. Если из поля Р исключить ноль, т.е. рассмотреть множество 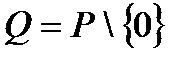, то относительно перенесённых на это множество операций умножение из поля Р, множество 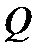представляет собой мультипликативную группу.

1. В поле нет делителей нуля.

2. Все числовые поля – бесконечные множества.

Date: 2015-09-02; view: 598; Нарушение авторских прав