Вопрос №3: Обратная матрица: определение, теоремы о существовании и единственности обратной матрицы

Рассмотрим квадратную матрицу

A =.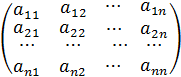

Обозначим Δ = det A.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0.

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Матрица, обратная матрице А, обозначается через А^-1, так что В = А^-1. Обратная матрица вычисляется по формуле

А^-1 = 1/Δ , (4.5)

где А_ij - алгебраические дополнения элементов a_ij.

Теорема. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.

Доказательство:1) Необходимость: так как А*А^-1=Е, то

2)Достаточность: зададим матрицу А^-1 в следующем виде:

.

Тогда любой элемент произведения 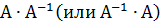, не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца матрицы А на алгебраические дополнения к элементам другого столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны Таким образом,

Теорема доказана

Вопрос №4:Системы линейных алгебраических уравнений (СЛАУ): скалярная и матричная формы записи. Правило Крамера. Решение и исследование СЛАУ методом Гаусса. Решение матричных уравнений с помощью обратной матрицы.

СЛАУ в матричной форме записывается в виде

AX = B, (1)

где

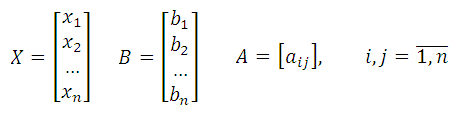
В скалярной форме записи

Система (1) имеет единственное решение, если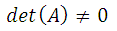

Правило Крамера:

Рассмотрим СЛАУ из n уравнений с n неизвестными (СЛАУ n-го порядка):

Для простоты изложения ограничимся сначала СЛАУ 3-го порядка

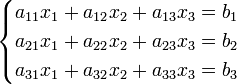
Определители:

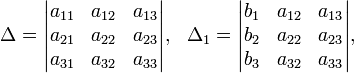
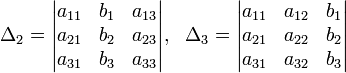
Справедлива следующая теорема (правило Крамера). Если определитель основной матрицы СЛАУ отличен от нуля,

то эта система имеет единственное решение, которое определяется формулами (формулы Крамера):

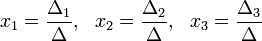
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

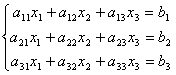Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а ₂₁ и умножим на – а ₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а ₃₁ и умножим на – а ₁₁, а затем сложим с первым. В результате исходная система примет вид:

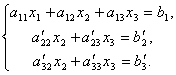
Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на 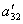, умножим на 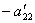и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1.перестановка строк или столбцов;

2.умножение строки на число, отличное от нуля;

3.прибавление к одной строке другие строки.